Po savaitės mano antrakursiai laikys pirmąją egzamino dalį. Šiandien repetavome. Man patiko du uždaviniai, kurie kažkaip iš kažkur atėjo į galvą. Ir jums patiks!
***
Pirmasis uždavinys. Kortų malkoje (kas per žodis! bet negalima sakyti kaladėje…) yra 32 kortos. Pradedantysis iliuzionistas žiūrovams sako:
– Ištrauksiu atsitiktinę kortą ir tai bus čirvų tūzas!
(Patyręs iliuzionistas klaustų žiūrovų, kurią kortą ištraukti…)
Visų akivaizdoje iliuzionistas sumaišo kortas ir iš atsitiktinės malkos vietos ištraukia čirvų tūzą. Kokia tikimybė, kad toje malkoje vien tik čirvų tūzai ir yra?
*
Sprendimas. (Man pačiam smalsu…). Iškeliame hipotezes, kad kortų malkoje yra vienas čirvų tūzas, du tūzai, trys, …, trisdešimt du. Taikome pilnosios tikimybės formulę:
P(A)= 1/32*1/32+1/32*2/32+1/32*3/32+…+1/32*31/32+1/32*32/32 = 1/(32*32)*(1+2+…+32)=1/(32*32)*(33*32/2)=33/64.
Taikome Bejeso formulę:
P(H32/A)= (1/32)/(33/64)=2/33.
Ne tokia jau didelė tokios apgavystės tikimybė…
***
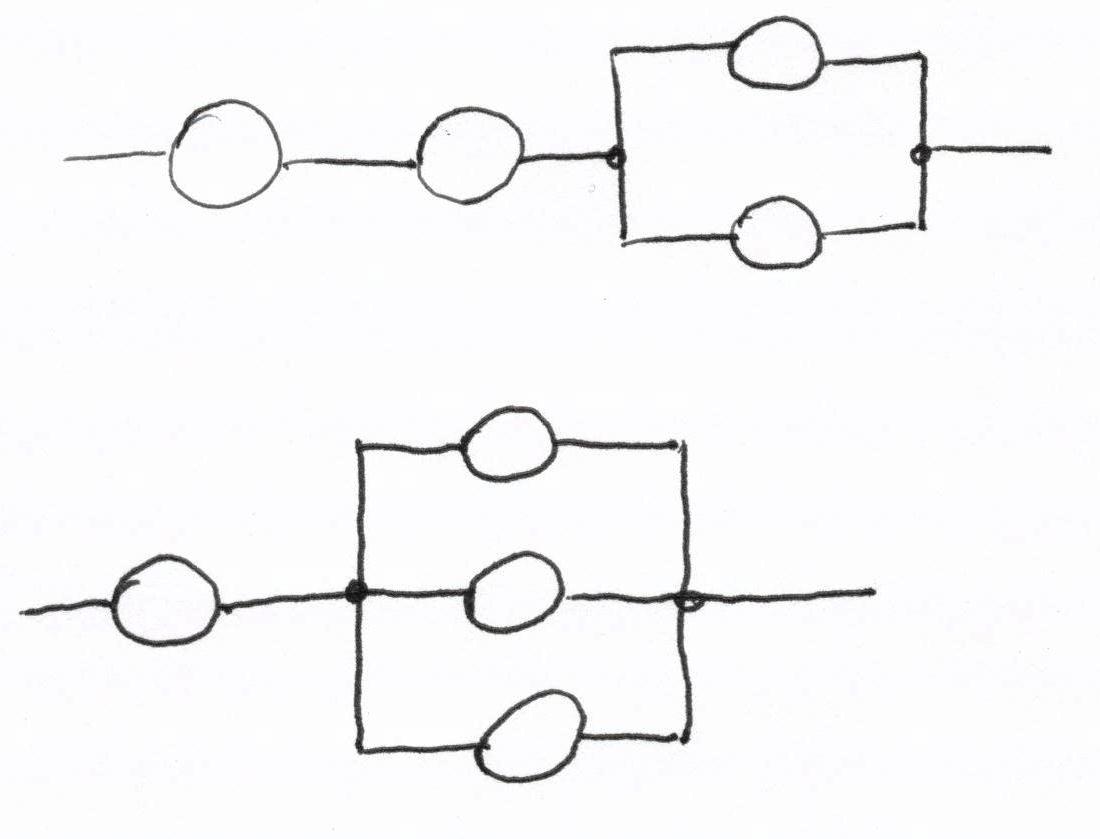
Antrasis uždavinys. Yra dvi grandinės (pažiūrėkite, kaip nevykusiai aš jas nubraižiau…). Kiekvieno elemento patikimumas (tikimybė nesugesti) yra p. Įrodykite, kad antroji grandinė patikimesnė (tarkime, tekės srovė nuo pradinio iki galinio taško). Tuo pačiu įrodysime, kad lygiagretus junginys patikimumas didina, o nuoseklusis – mažina.
*
Lakoniškas, miglotas sprendimas. P(A)= p*p*p+p*p*p-p*p*p*p = 2p^3-p^4.
P(B)=p*p+p*p+p*p-p*p*p-p*p*p-p*p*p+p*p*p*p=3p^2-3p^3+p^4.
2p^3-p^4<3p^2-3p^3+p^4;
2p-p^2<3-3p+p^2;
2p^2-4p+3>0.
Dabar jau patys išspręskite šią kvadratinę nelygybę…
Taip ir ruoškitės egzaminui, jaunieji mano kolegos!
Atsakymai
Burgis, 2012-03-19 14:20:22
Ačiū?…
Saulius, 2012-03-19 16:42:44
O iš kurios pusės pro elementus srovė teka ?
petras, 2012-03-19 16:59:36
Sauliau, nėra skirtumo.
o pirmas uždavinys tai keistai suformuluotas kažkaip, nervina mane 🙂
Saulius, 2012-03-19 17:46:40
..hmm…… imkim antrą pav.
Na jei srovė teka teka… iš kairės ir betekėdama jau sugadina pirmą elementą, tai nebepadės ir sekantys trys.
O jei srovė teka teka… teka ir teka iš dešinės. Ir pritekėjusi sugadina vieną iš trijų pirmų elementų tai dar yra galimybė kad ji nutekės iki galutinio taško.
Ar ne taip ?
Žydrūnas, 2012-03-19 19:36:40
tai ir taip matosi, kad antra patikimesnė 🙂
na aš iš praktikos žinau, bet aišku gali būti sudėtingesnių variantų kur taip nesimato..
reik pasimokyt gal 🙂
Burgis, 2012-03-19 20:36:12
Tos schemos yra „matematinės“, ten elementai kažkaip sugenda nepriklausomai vienas nuo kito… Kitaip studentams būtų per sunku.
sqrt, 2012-03-19 21:04:59
Pirmasis uždavinys yra nekorektiškas, nes nėra duotas iliuzionisto “malkos” pasiskirstymas.
Direktoriaus sprendimas tariant, kad variantai su 1, 2, …, 32 tūzais yra vienodai tikėtini yra toks pat fokus marokus kaip ir nagrinėjamas pasirodymas ant scenos 🙂
Burgis, 2012-03-19 21:43:44
sqrt: Jūsų pirmasis teiginys prieštarauja antrajam…
Pentium100, 2012-03-19 23:23:11
Sutinku su sqrt dėl pirmojo uždavinio. Ne tik kortų malkoje gali būti daugiau nei viena reikalinga korta, dar ir maišymas gali būti netikras.
http://www.youtube.com/watch?v=MZI8Pn8kxCI
sqrt, 2012-03-20 08:54:34
O kokiu būdu prieštarauja? 🙂 Aš abu juos sudėjęs į vieną gaunu visai gražų teiginį: nekorektiškus uždavinius galima išspręsti tik fokus marokus būdu.
Pavyzdžiui, galima tarti, kad pradedantysis Iliuzionistas (pagrįstai) abejoja savo sugebėjimais, tad ruošdamasis pasirodymui visuomet ima kortų malką sudarytą iš vienų tūzų. Tuomet ieškoma tikimybė bus lygi 1.
Arba galima tarti, kad jis kortų kaladę perka atsistiktiniame kioske autobusų stotyje. Tuomet ieškoma tikimybė bus lygi 0. (Nes kioskai kortas pardavinėja atsakingai)
Ir apskritai, bet kuriam norimam atsakymui galima sugalvoti pasiskirstymą ir tą atsakymą gauti. Tai, kad skaičiuojama ‘posterior’ tikimybė (gal žinote gražų vertimą?) tik maskuoja faktą, jog šitame uždavinyje yra klausiama klausimo panašaus į “Petriukas tik jam žinomu būdu pasirinko 32 skaičius nuo 1 iki 13. Kokia tikimybė, kad jie visi lygūs 1?”. Kadangi mes nežinome, kaip Petriukas skaičius renkasi, tai nežinome ir tikimybės.
Dominykas, 2012-03-20 11:23:59
Išties, pirmas uždavinys prajuokino. Maždaug, Lietuvoje gyvena 3 milijonai gyventojų. Atsitiktinai vieną pasirinkus, randam negrą. Kokia tikimybė, kad Lietuvoje visi negrai? Smagioji dalis, jog pakeitus “Lietuva” į pvz. “Namibija”, atsakymą gaunam tokį patį ,)
petras, 2012-03-20 14:51:58
Sauliau, tai ar iš dešinės ar iš kairės tekės elektra. vis tiek apatinė grandinė yra patikimesnė.
Dominykai geras pavyzdys 😀
Audrius, 2012-03-21 13:00:48
sqrt: dėl žodžio ‘posterior’. Nežinau, kiek gražus jo vertimas:), bet kartą teko naudoti Bayes’o formulę… kurioje šis terminas taip pat yra. Pagal prasmę žodį “Posterior probability” vartojau kaip “atskiro įvykio atsikartojimo (intensyvumo, jei tai procesas laike) tikimybę”. Trumpai paaiškinant, tai yra tikimybė, kuri parodo, kokia dalimi atkartota apriorinė atskiro įvykio tikimybė.
Burgis, 2012-03-21 14:14:13
Audriui: taip, tikimybės būna apriorinės ir aposteriorinės…
Audrius, 2012-03-21 14:44:36
Gerb. Direktoriui: Taip, tokios yra:). Tiesiog naudojau apriorinę, kaip atskiro įvykio pasirodymo (atsikartojimo) tikimybę. Tiesiog buvo žinoma charakteristikos skaitinė vertė, kuri priklauso nuo atskirų sistemą sudarančių įvykių. Aišku, kad atskirų įvykių apriorinių tikimybių suma =1; atskirų hipotetinių įvykių tikimybių suma =1; bet va, minėtoji vieno atskiro įvykio (iš keleto) atsikartojimo tikimybė („posterior probability“) 1, kas parodo pasirinkto matematinio modelio tikslumą.
Audrius, 2012-03-21 14:47:41
…atsikartojimo tikimybė („posterior probability“) daugiau už 1, kas parodo pasirinkto matematinio modelio tikslumą. Pasimetė ženklas “daugiau”… Na, tiek to, užteks kiek yra:)
sqrt, 2012-03-21 19:06:32
Aha, žodžiu kandidatas “aposteriorinė”, matau ir vikipedijoje toks terminas įrašytas. Turėsiu omenyje, nors norėtųsi gražesnio žodžio, angliški “prior” ir “posterior” daug elegantiškesni.
Audrius, 2012-03-22 10:50:46
Žinoma, bus nurodyti žodžių „apriorinė” ir “aposteriorinė” paaiškinimai, todėl minėti terminai neturėtų sukelti didelių rūpesčių. Be to, trumpesnis, lakoniškesnis pavadinimas lengviau įsimenamas, taip pat gerai siejasi su angliškaisiais terminais. Manau, kad elegancijos elementas turės atsispindėti lietuviškose šių terminų apibrėžtyse:). Taip. Pagarbiai…