Grįžtu prie ankstesnės temos:
***
Mokytoja:
Patarkite kaip racionaliau išspręsti uždavinį:
teatro ložėje vienoje eilėje yra 6 vietos. Pertraukos metu žiūrovai gali išeiti į holą iš abiejų pusių. Kokia tikimybė, kad bent vienas žiūrovas, norėdamas išeiti, turės paprašyti praleisti kurį nors iš šioje eilėje sėdinčių žiūrovų?
***
Sokolovas:
Mokytojai
Iš pradžių randame priešingo įvykio (visi 6 išeis „be kliūčių“ ) tikimybę:
(2/6)(2/5)(2/4)(2/3)(2/2) = 32/720=2/45
Tuomet mus dominančio įvykio tikimybė:
1- (2/45)=43/45
***
Burgis:
Raskite klaidą mano samprotavimuose…
Tarkime, kol kas, kad eilėje yra ne šeši, o tik keturi žiūrovai. Sėdintį pertraukos metu žiūrovą pažymėkime nuliu, atsistojusį išeiti – vienetu. Akivaizdu, kad yra šešiolika situacijų, kurios gali susidaryti pertraukos metu: nuo tokios, kai niekas iš savo vietų nepakyla, iki tokios, kai visi atsistoja ir nori išeiti pasivaikščioti.
*
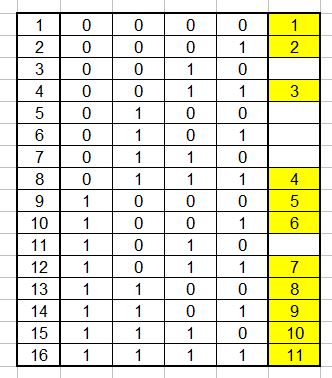
*
Suprantama, kad ir pirmuoju, ir antruoju atveju niekas nieko prašyti praleisti neturi.
Iš viso yra 11 situacijų, kai išeinantys pasiliekančių sėdėti neturi prašyti praleisti. Kad bent vienas turės prašyti praleisti, tikimybė yra 1- 11/16=5/16.
Jei eilėje yra penkios vietos, ta tikimybė yra 1-16/32=1/2.
*
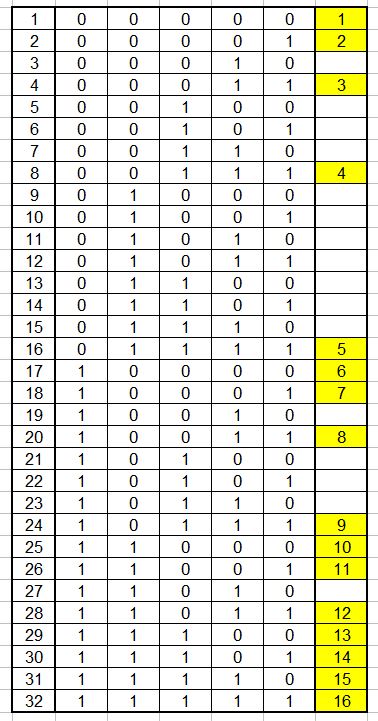
*
Jei eilėje yra šešios vietos, ta tikimybė yra 1-24/64=5/8.
Matome, kad žmonių skaičiui eilėje didėjant, tikimybė didėja, bet Sokolovo pateiktas atsakymas neįtikina – aš esu buvęs teatre…
Atsakymai
Burgis, 2015-04-14 11:05:05
Vis tiek ji sukasi!… 🙂
Sokolovas, 2015-04-14 12:37:54
Gerb. Burgiui:
Akivaizdu tai, jog uždavinio sąlyga nėra išsami. Tuo tarpu, jei formuluotė “viską aiškintų”, uždavinio tekstas taptų labai ilgas…
Spręsdamas laikiau, jog
-
Išeiti turi VISI šeši ( arba keturi jūsų variante).
-
Žmonės išeina PO VIENĄ.
Tai “savivalė”? Gal…Bet, o kodėl Jūs darote prielaidą, jog, pavyzdžiui, du ( ar trys, ar keturi) žiūrovai išeina VIENU METU, ir tai priskiriate elementariems įvykiams, palankiems įvykiui “nei vienas neturės prašyt kitų jį praleisti”? Kodėl?
Burgis, 2015-04-14 12:52:49
Sokolovui: todėl, kad aš esu buvęs teatre…
petras, 2015-04-14 12:58:55
Radau klaidą 🙂 tuo atveju kai visi atsistoja eiti pasivaikščioti, gali prašyti praleisti, nes gali į skirtignas puses bandyti eiti, juk pradinėje sąlygoje parašyta, kad per abi eilės puses galima išeiti 😉
petras, 2015-04-14 13:02:14
aij ten tik sėdančių reik prašyt praleit. vėl neperskaičiau iki galo sąlygos. ieškau toliau 😀
Sokolovas, 2015-04-14 13:03:15
JEI LOŽĖJ BUVO KETURI ŽMONĖS
Išeina po vieną. Išeit turi visi.
Įvykis A- nei vienas neturės kitų prašyt jį praleisti.
Sprendžiant mano pateiktu būdu, gauname:
P(A) = (2/4) (2/3)(2/2) = 8/24 = 1/3
Dabar išspręskime gerb. Burgio būdu, t.y. rašydami elementariuosius įvykius.
Skaičiumi 1 pažymėkime pirmąjį išeinantį, skaičiumi 2-antrąjį, skaičiumi 3 -trečiąjį, skaičiumi 4- ketvirtąjį.
Įvykiui A palankių elementariųjų įvykių yra AŠTUONI. Štai jie:
1, 2, 3, 4
4, 3, 2, 1
2,3, 4, 1
1, 4, 3, 2
2, 4, 3, 1
1, 3, 4, 2
3, 4, 2, 1
1, 2, 4, 3
Visų elementariųjų įvykių skaičius 4! = 24. Jų visų nerašau. Tarp įvykiui A nepalankių elementariųjų įvykių yra, pavyzdžiui
2, 1, 3, 4
3, 1, 2, 4, ir t.t.
Tad P(A) = 8/24 = 1/3
Sokolovas, 2015-04-14 13:16:02
KARTOJASI ĮŽYMIOJI DALAMBERO KLAIDA?
Gerb. Burgis buvo teatre, o Dalamberas kadaise mėtydavo monetą…Tikimybių teorijos aušroje…
Ir jis tikino ( ir to neatsižadėjo iki paskutiniosios…), esą tikimybė, jog metus dvi monetas, abu herbai atvirsta su tikimybe 1/3.
Jis elementariuosius įvykius formulavo taip: atvirsta ABU herbai, atvirsta VIENAS herbas, atvirsta NEI VIENO herbo.
Kur čia klaida? Esmė tai, jog Dalamberas neatsižvelgė į tai, kad jo formuluojamos baigtys NĖRA VIENODAI TIKĖTINOS, ir tokiu atveju negalima taikyti klasikinio tikimybės apibrėžimo.
Ar čia- ne tas pats?
Gerb. Burgi, jūsų samprotavimai grindžiami principu- “noriu einu, noriu neinu”. Be to, nori – kartu išeina du asmenys, nenori- išeina po vieną ( jūsų du identiški “vienetukai” į pastarąjį “norą-nenorą” kaip ir neatsižvelgia…). Taigi, AR JŪSŲ SURAŠYTOS BAIGTYS YRA VIENODAI TIKĖTINOS?
Tikimybės apibrėžimą čia galima taikyt tik tuo atveju, jei žiūrovus prilyginsime…RUTULIAMS DĖŽĖJ, ar knygoms lentynoje. Jie (jos) nesirenka, “išeit ar likt”, jie TRAUKIAMI IŠ DĖŽĖS.
O prieš subjektyvumą ( “rutulys nenori išlįst iš dėžės) tikimybių teorija bejėgė 🙂
Burgis, 2015-04-14 13:21:27
Sokolovui: užjaučiu Jus, bet padėti nebegaliu…
Primenu, kad aš jau grįžau, kad svetainė mano, kad Jūsų komentarus netrukus imsiu trinti, nes Jūs manęs neklausote…
Sokolovas, 2015-04-14 13:27:16
Gerb. Burgiui:
Čia Jūsų svetainė. Ar trint, ar palikt mano komentarus- Jūsų valia. Niekad nebuvau dėl to Jums priekaištavęs. Dėkoju už galimybę padiskutuot matematikos klausimais.
Su pagarba.
Burgis, 2015-04-14 13:29:41
Sokolovui: ir aš šio to nesuprantu: 2,3, 4, 1 – Jūsų variantas išeiti be atsiprašymo. Pro kur išeina 2, jei nė vienas dar neišėjęs?
Sokolovas, 2015-04-14 13:37:47
Gerb. Burgiui:
Skaičius rodo ne konkretų žmogų, o “išėjimo eilės” numerį. Ši bandymo baigtis tokia:
Pirmasis išėjo dešiniajam krašte sėdėjęs žmogus, po to ( antras išėjo)- iš kairiojo krašto, po to ( trečiasis) išeina pro jau atsilaisvinusį kairįjį kraštą ( kelias jau laisvas), ir likęs žmogus išeina.
Burgis, 2015-04-14 13:52:50
Sokolovui: na, man atrodo, kad iš didelio rašto Jūs jau išėjote už krašto! Kaip tai „išėjimo eilės numerį“ rodo, jei Jūs parašėte, kad „visi išeina po vieną“?! tai visada pirmas išeina pirmas, antras išeina antras… Ne, Jūs geriau pagalvokite prieš rašydamas…
*
O dabar man, prašyčiau, tą patį aštuonių įvykių sąrašą pateikti man suprantamu būdu: numerius žiūrovų ta tvarka, kaip jie vienas po kito išeina. Jei neklausysite, ištrinsiu visus Jūsų komentarus, reikia baigti tuos cirkus!
Sokolovas, 2015-04-14 14:16:14
Gerb. Burgiui
Tai todėl ir galima kalbėt apie išėjimo eilės numerį, kad po vieną išeina…Gerai, pateiksiu kitaip…
Buvo keturi žmonės
A, B, C, D ( tokia tvarka jie sėdėjo)
Mano anksčiau pateikti elementarieji įvykiai:
-
Išeina A, po to B, po to C, po to D.
-
Išeina D, po to C, po to B, po to A
3 Išeina D, po to A, po to B, po to C
4 Išeina A, po to D, po to C, po to B
5 Išeina D, po to A, po to C, po to B
6 Išeina A, po to D, po to B, po to C
7 Išeina D, po to C, po to A, po to B
8 Išeina A, po to B, po to D, po to C
Burgis, 2015-04-14 14:28:18
1, 2, 3, 4 – A, B, C, D – tinka
4, 3, 2, 1 – D, C, B, A – tinka
2,3, 4, 1 – B, C, D, A – netinka! Jūsų pataisytame variante yra D, A, B, C – tinka!
1, 4, 3, 2 – A, D, C, B – tinka
2, 4, 3, 1 – B, D, C, A – netinka!
1, 3, 4, 2 – A, C, D, B – netinka!
3, 4, 2, 1 – C, D, B, A – netinka!
1, 2, 4, 3 – A, B, D, C – tinka
***
-
Išeina A, po to B, po to C, po to D.
-
Išeina D, po to C, po to B, po to A
3 Išeina D, po to A, po to B, po to C
4 Išeina A, po to D, po to C, po to B
5 Išeina D, po to A, po to C, po to B
6 Išeina A, po to D, po to B, po to C
7 Išeina D, po to C, po to A, po to B
8 Išeina A, po to B, po to D, po to C
*****
Neišsisukinėkite, Sokolovai, jei parašote neteisingai ar visai nesuprantamai – reikia pripažinti. Bet gal aš klystu? Raidiniai variantai visi geri. Tai gal skaitiniai variantai yra kažkaip mistiškai užkoduoti?
***
Jūs galite man vieną kartą atsakyti ir šią diskusiją baigiame!
Sokolovas, 2015-04-14 14:34:45
Gerb. Burgiui:
Dėkui. Bet raidinius variantus aš, rašydamas Jums, nurašiau nuo skaitinių…:)
Varianto B, C, D, A pas mane nėra ir nebuvo…
Burgis, 2015-04-14 14:47:43
Ne, Sokolovai, aš taip negaliu palikti… Tegu pyksta kiti lankytojai, bet Jūs man paaiškinkite: pirmoje ir antroje eilutėje 2 reiškia B, trečioje eilutėje 2 reiškia D? Kodėl?!
Sokolovas, 2015-04-14 16:24:01
Gerb. Burgiui:
Pirmoje eilutėje ( 1, 2, 3,4) turėta omeny, jog A išeina pirmas, B- antras, C- trečias, D- ketvirtas. Ta prasme rinkinį ( 1, 2, 3, 4) atitinka rinkinys A, B, C, D.
Antrojoje eilutėje ( 4, 3, 2, 1) turėta omeny, jog A išeina ketvirtas, B- trečias, C- antras, D- pirmas. Ta prasme rinkinį ( 4, 3, 2, 1) atitinka rinkinys D, C, B, A
Trečioj eilutėj ( 2, 3, 4, 1) turėta omeny, kad A išeina antras, B- trečias, C- ketvirtas, D- pirmas. Gauname rinkinį D, A, B, C.
Iš viso to tikrai neišplaukia, jog “2 reiškia B arba D…”. Tai buvo skirtingi elementariųjų įvykių formulavimai….
Adefagija, 2015-04-14 16:31:26
Ką čia dabar reikia ginčytis, jeigu visur ir visada galioja Merfio dėsniai…
Tai ir šiuo atveju, kraštiniai žiūrovai pertraukos metu greičiausiai liko sėdėti, o myšt ir parūkyt užsimanė tie, kur sėdėjo apie vidurį.
Tik išeinantys ir sugrįžtantys turėtų atsiminti, kad išilgai žiūrovų eilės yra slenkama atsisukus veidu, o ne užpakaliu į žmones.
Tai va, tiek čia tos matematikos.
*****
Klausimas Burgiui: kodėl aš, vienintelė iš jūsų svetainės svečių, turėjau gedėti kažkokio jūsų advokato?
Stebėtoja, 2015-04-14 16:45:38
Adefagija, tu vienintelė, kuri įsimylėjusi B.Burgi ir tai akivaizdu. B.Burgis taip pat, bet slepia tai nuo žmonos, todėl “ištrina” tavo komentarus, bet norėjo, kad tu gedėtum kartu. Tai normalu. Tai MEILĖ. Tikra meilė.
Adefagija, 2015-04-14 17:15:28
Bet gi aš tai to advokato nebuvau girdėjusi, tik žinau, kad jo labai menkas stažas,…Tai iš kur jis garsus tada? – Kad vieną garsų pijoką išsuko iš kalėjimo? Tiesa, prieš advokatūrą dirbo VSD ir didžiąją Lietuvos teroristę E. Kusaitę, pašėrė kažkokiais negerais saldainiais, gal dėl to garsus?
O kad nusišovė, tai negedėt reikia, bet džiaugtis, kad žmogui sumanymas pavyko iš pirmo karto.
Stebėtoja, 2015-04-14 17:23:06
Garsus, nes buvo pirmas B.Burgio byloje.
Adefagija, 2015-04-14 17:32:05
Tai B.Burgis ir padarė esminę klaidą, kad advokatą pasirinko pagal garsumą, o ne pagal profesionalumą.
Geras advokatas būtų pabaigęs bylą ikiteisminio tyrimo stadijoj ir ne su tokiais praradimais….
Burgis, 2015-04-14 17:37:22
Sokolovui: ačiū, dabar aišku. Dabar jau tikrai baigiame tą diskusiją, nes kiti lankytojai išsilakstys… Ateityje, kaip ir prašiau, rašykite ne daugiau kaip tris komentarus per dieną ir ne daugiau kaip po 7 eilutes. Reikia gerbti visus. Ačiū.
Burgis, 2015-04-14 17:39:03
Adefagijai: tik aš Jūs pagyriau, o Jūs vėl savo… Tai nejaugi negalite normaliai diskutuoti, o ne „išsidirbinėti“? Nei Jūsų, nei kitų neprašiau gedėti, prašiau neteršti svetainės, nes neturėjau nei noro, nei galimybės ją valyti.
Vilniete, 2015-04-14 17:43:11
Tai čia gi matematinė tema, kodėl bijot, kad lankytojai išsilakstys? Kaip tik įdomiau ir solidžiau, kai daugiau komentarų. Pasiginčyčiau ir aš apie matematiką, net gaila, kad ne kažką suprantu -). Tačiau pasiskaitau su malonumu.
Stebėtoja, 2015-04-14 18:47:17
Čia ,manau viskas ” Šiaip sau, iš dyko buvimo…”:)
Vilniete, 2015-04-14 19:10:53
O Sokolovas rimtai :-). Nuostabus žmogus. Aš be ironijos.
Mokytoja, 2015-04-14 20:05:11
Gerb. direktoriui ir Sokolovui: ačiū už išsamų uždavinio sprendimą. Labai džiugu, kad yra matematikos tema, kurioje galima patarimą gauti ar bent padiskutuoti 🙂
Burgis, 2015-04-14 21:19:54
Ačiū, Mokytoja!
Trakimas, 2015-04-14 22:15:28
Tce renkasi ta pati publika,kuri trolino ir Raco bloge:)O Racas baige liudnai-dabar jis nebera BNS direktorium ,o yra “faktu ” redaktorium,reporteriu ir valytoju viename.
Trakimas, 2015-04-14 22:20:42
O ka veikia Valatka?Po Snoro sunaikinimo?O ka veikia Janutiene,ishmesta ish tv 3?Burgis taip pat uzkliuvo kazkam.Ash labai ilgai laukiaiu “adefagijos” komentaro apie Burgio advokata -buvusi VSD antiteroristinio padalinio vada:)Perskaiteu ji ir man viskas tapo aisku:)O Jums,gerb.Burgi?
apropos, 2015-04-15 06:49:35
Kažin, jau visi išsisprendėt sau šitą visur platinamą uždavinį? Stebiuosi, kad jis čia dar neaptarinėjamas
“Albert and Bernard just become friends with Cheryl, and they want to know when her birthday is. Cheryl gives them a list of ten possible dates:
May 15
May 16
May 19
June 17
June 18
July 14
July 16
August 14
August 15
August 17
Cheryl then tells Albert and Bernard seperatly the month and the day of her birthday respectively.
Albert: I don’t know when Cheryl’s birthday is, but I know that Bernard doesn’t know too.
Bernard: At first I don’t [sic] know when Cheryl’s birthday is, but I know now.
Albert: Then I also know when Cheryl’s birthday is.
So when is Cheryl’s birthday?”
Andrius, 2015-04-15 07:40:50
Tik išeinantys ir sugrįžtantys turėtų atsiminti, kad išilgai žiūrovų eilės yra slenkama atsisukus veidu, o ne užpakaliu į žmones.
O ar įmanoma tai sklandžiai padaryti siauruose praėjimuose tarp eilių?
Burgis, 2015-04-15 09:19:48
Cheryl’s gimtadienis turėtų būti rugpjūčio 17 d.
*
Raskite klaidą mano samprotavimuose:
*
-
Iš to, ką pirmu sakiniu pasakė Albertas išplaukia, kad jam (Albertui) negalėjo būti pasakytas nei gegužės, nei birželio mėnuo, nes priešingu atveju Bernardui galėjo būti pasakytas skaičius 19 arba 18, o tai vienareikšmiai apibrėžia gimimo datą. Vadinasi, Alberto tvirtinimas rodo, kad šis vyrukas numatė, jog Bernardui negalėjo būti pasakyta nei 19, nei 18.
-
Iš pirmojo Alberto teiginio Bernardas padarė išvadą, kad Albertui buvo pasakytas liepos arba rugpjūčio mėnuo. Žinodamas, kad jam pasakytas skaičius 17, Bernardas ir pasakė, kad jau žino gimimo datą. O tada ir Albertas suprato, kodėl Bernardas žino gimimo datą.
***
Na, tinka?
apropos, 2015-04-15 10:16:24
Mačiau feisbukuose, kad buvęs jūsų moksleivis Nerijus Mačiulis sugaišo šitam uždaviniui 10 minučių ir gavo atsakymą July 16. Šiaip plinta mitai, kad tai Singapūro 10 metų moksleiviams skirta užduotis. Bet yra ir kitas variantas, kad vis dėlto 14-mečiams, ir dar olimpiadininkams.
Burgis, 2015-04-15 10:20:03
apropos: na, aš irgi sugaišau apie 10 minučių, bet, matyt, išsprendžiau neteisingai, tačiau klaidos neieškosiu… Tegu kiti ieško.
petras, 2015-04-15 10:46:18
mano nuomone, tai mačiulis teisus. nes bernardas kai sako, kad jis žino kada yra gimtadienis, tai jis gali turėti skaičius 16,15 ir 17 plius iš Alberto sužinojo, kad netinka gegužė ir birželis, todėl 19,18 ir 14 negali turėti nes 19 ir 18 patenka į gegužę ir birželį, o 14 d. patenka į liepą ir rugpjūtį. taigi tinka 16 diena, nes paskutinis žodį taria albertas ir pasako, kad jau ir jis žino, taigi lieka tik liepos 16 d. nes 15 ir 17 dienos abi patenka į rugpjūtį, taigi jei būtų rugpjūtis pas albertą, jis nežinotų gimtadienio dienos. kaip supratau fokusas tame, kad Bernardas sužino gimtadienio dieną anksčiau už albertą ir už mus. o mes sužinome gimtadienio dieną tik kai jau albertas pasako, kad ir jis žino. fainas logikos uždavinys 🙂 šiaip internete panašaus stiliaus uždavinių plačiai paplitę yra daugiau ( iš serijos, tokius uždavininius sprendžia singapūro 7b klasės mokelseiviai :))
aina na, 2015-04-15 14:05:41
Adefalija,
Norejau spaust tau PLIUSĄ , bet nepasispaudžia. Gal sitame tiklarastyje uždrausta tave “LAIKINT” ?
aina na, 2015-04-15 14:12:14
Adelija,
Veidu į priekį aš slinkt negaliu. Prie kokios 4-tos damos jau bunu susijaudines ir kliunu už likusių ant praejimo ?
Ka daryt?
Adefagija, 2015-04-15 16:36:49
aina na: apsiauk tampresnėm kelnaitėm (gali ir dvejom, trejom, tik kad nebutu išsitase); praslink užsimerkęs; slinkdamas mintyse skaičiuok avis iki šimto; prašuoliuok šoniniu galopu, kad nespetum jaudintis…Ir pastoviai gerk kmynų arbatą – sako padeda.
Burgis, 2015-04-15 16:48:11
Petrui: teisingai, tai liepos 16 diena.
Kai Albertas pasakė, kad aš nežinau, bet ir Bernardas nežino, tai Bernardas suprato, kad Albertas turi liepos, o ne rugpjūčio mėnesį (nes jei Albertas būtų turėjęs gegužės arba birželio mėnesį, tai nebūtų galėjęs garantuoti, kad Bernardas nežino: turėdamas 19, Bernardas žinotų, kad tai gegužė, turėdamas 18, žinotų, kad tai birželis). Albertas „blefavo“dėl liepos ir rugpjūčio, bet Bernardas turėjo 16, todėl iškart pasakė, kad žino datą (liepos 16), o tada ir Albertas suprato, kad žinoti galima tik liepos 16, o ne kitą dieną.
miklis, 2015-04-15 17:39:30
Šitą temą linksma skaityti. Čia įmanoma rasti ir gerų galvosukių, ir įvairaus gero, bet susimąstyti verčiančio jumoro. Burgio ir Sokolovo dvikova tai jau visai arši pasidarė, irgi juoką kelia. Tiesa, Sokolovo viena mintis apie Dalambero klaidą man tikrai patiko. Skaičiuojant tikimybes turi būti išlaikytas vienodas tikėtinumas, o tai dažniausiai neįmanoma. Iš principo, žmogiškasis faktorius matematikoje man atrodo ignoruojamas (tai ne mano mintis, bet vienas žmogus mane įkvėpė taip galvoti). Todėl čia pat atsiranda Adefagija, kuri griežtai spręsti nelabai moka, bet viską paaiškina žmogiškai, turėdama minty, kad bandymas išspręsti uždavinį griežtai matematiškai tėra paistalai, nes neatsižvelgėme, kad elementariesiems (vienodai tikėtiniems) įvykiams priskyrėme tuos, kurie iš tikrųjų nėra elementarieji. Tai logiška paprasčiausiai vien dėl to, kad per vidurį eilėje sėdintys žmonės dažniausiai neišeidinės lygiai tiek, kiek kraštiniai. Bet juk tai ir buvo Dalambero klaida.
miklis, 2015-04-15 18:04:19
Kiti kelia, tai ir aš įkelsiu kelias gražesnes užduotėles, kurias teko man spręsti pastarąją savaitę.
-
Duota, kad valtis upe prieš srovę nuplaukė tam tikrą atstumą, o po to apsisuko ir pasroviui nuplaukė k² didesnį atstumą. Įrodyti, kad ji sugaiš mažiausiai laiko tada, kai upės tėkmės greitis bus toks, kad pasroviui valtis plauktų k kartų didesniu greičiu, nei prieš srovę.
-
Duotas rombas, kurio smailusis kampas A, o įbrėžto apskritimo centras r. Rasti rombo plotą.
-
Yra 8 skirtingos naujametinės dovanos, kurias 2 Kalėdų seneliai (Sanas ir Santa) turi pasidalinti ir įteikti vaikams. Kiekvienas iš Kalėdų senelių turi įteikti nemažiau kaip dvi dovanas. Įrodyti, kad dovanas jie gali pasidalinti 238 būdais.
Sokolovas, 2015-04-15 19:12:17
Gerb. Mikliui:
Šaunuolis! Aš irgi manau, kad žmonės turi daugiau domėtis matematika, ir uždavinių reikia kuo daugiau. Dėkui!
Pirmasis uždavinys- išvestinės taikymas. Naudinga abiturientams, artėjant egzaminui…
Antrame uždavinyje r yra apskritimo spindulys, o ne centras. Nebūtina nurodyt, kad A yra smailusis rombo kampas. Tiesiog- vienas rombo kampas. Atsakymas
S=4 r r / sinA nuo to nepriklauso.
Trečias uždavinys- derinių skaičiaus bei kombinatorinės sudėties taisyklės taikymas. Beje, jis bus dar lengvesnis tiems, kas išmano Niutono binomą 🙂
Atsakymas, 2015-04-15 19:36:46
Sokolovui: o aš manau, kad daugiau žmonių turi griežti smuiku. Ir ką?
miklis, 2015-04-15 22:38:02
Turi būti ir tų, ir tų. Galiausiai, juk pačiame smuiko garse nemažai matematikos ir gražu, kai grojantysis tą bent truputėlį suvokia.
Pirmąjį uždavinį aš sugebėjau išspręsti labai algebriškai, bet be išvestinių, nors tikiu, kad su išvestinėm daug lengviau.