
Kaip aš tai padaryčiau?
(Gaila, beveik niekas nebesuteikia progos pabandyti…)
Kas nežino, kad kvadratinės lygties sprendimas yra viena svarbiausių matematikos temų mokykloje?
Kaip tą temą pateikti?
Įsivaizduokite, kad tai jau ne pirmoji pamoka ta tema. Žiūrėkite į paveikslėlį ir skaitykite…
*
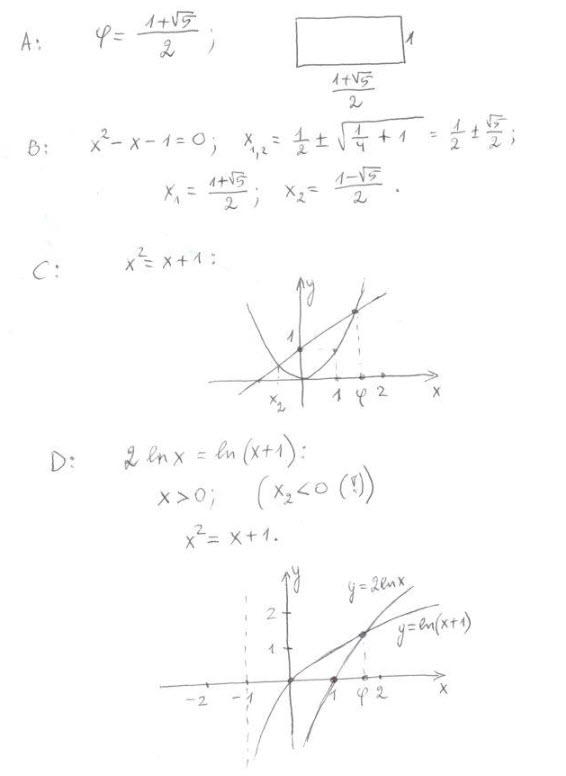
A: Užrašyčiau skaičių fi, parodyčiau gražiausią pasaulyje stačiakampį (panašiai tokį stačiakampį matote mano nuotraukoje „Įkalintas“) ir pasiūlyčiau internete susirasti viską apie „aukso pjūvį“, „dieviškąją proporciją“ (Golden Mean, Golden Section, Golden Ratio, Divine Proportion…)
*
B: Tada parodyčiau, kaip spręsti redukuotąją kvadratinę lygtį (be jokių ten „atskirai apskaičiuokime diskriminantą“!) ir tai, kad šios lygties vienas sprendinys ir yra fi.
*
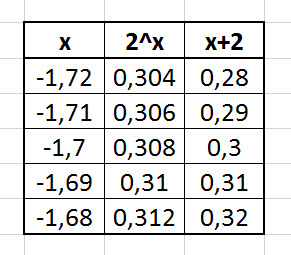
C: Tada parodyčiau, kaip grafiškai išspręsti tą lygtį ir kur yra tas fi. Papasakočiau, kas ta parabolė (nes mokytojai dažniausiai tai pamiršta pasakyti…). Į moksleivių klausimus (jei tokių būtų…), kodėl lygtį reikia spręsti grafiškai, atsakyčiau parodydamas paprastos transcendentinės lygties (pavyzdžiui, 2^x=x+2) sprendimą grafiškai; pasiūlyčiau namuose jį papildyti „sprendimu“, pavyzdžiui, Excel programa.
*
D: Vėl prie tos temos grįžčiau kitoje pamokoje, vyresniems gimnazistams, kai jie mokosi apie logaritmus. Parodyčiau, kaip svarbu nepamiršti apibrėžimo srities nelygybės ir kaip tai gražiai dera su grafiniu lygties sprendimu.
*****
Jei iki šios vietos perskaitei ir esi gimnazistas, gali man parašyti laiškelį adresu [email protected] – atsiųsiu tau trijų puslapių konspektą „Viskas apie trikampį“. Turiu laiko – negaliu nespręsti…
Atsakymai
Sokolovas, 2016-10-03 13:44:27
GRAŽIAUSIAS TRIKAMPIS
Trikampio ABC kraštinėje AB pasirinktas taškas D taip, kad <ABC = <ACD,
CA=BD, AD=1.
Apskaičiuokite atkarpos BD ilgį.
Burgis, 2016-10-03 14:32:14
Sokolovui: po dviejų dienų prašyčiau čia pateikti uždavinio sprendimą, kitaip sąlygą išmesiu… Aš juk viską išspręsdamas rodau, pastebėjote?
Sokolovas, 2016-10-04 09:37:24
STEBINA ABEJINGUMAS, OI STEBINA…
Stebina skaitytojų abejingumas šiai temai. Nejaugi neįdomu, negi nekyla minčių???
Nemokame matematikos? Bet juk ir matematikos mokytojai skaito gerb. Burgio portalą!
Taigi, vieni abejingi, nes “nemoka”. O kiti, nes jiems “ir taip viskas aišku…”
Liūdna gyvent, kai būna “viskas aišku…”
Aš nemoku Matematikos. Ir todėl man nėra liūdna. Aš tik mokausi didžiųjų to Mokslo Apsireiškimų, svajingų Penktojo išmatavimo paslapčių. Ir štai…
Apsireiškimas:
Kaip gimsta gerb. Burgio straipsnyje pateiktas Gražiausias stačiakampis:
O buvo taip: Duotas stačiakampis, kurio gretimų kraštinių ilgiai yra 1 bei a (a>1). Šalia šių stačiakampio kraštinių brėžiami du kvadratai. Aišku, jų plotai lygus 1 bei a^2.
Jeigu stačiakampio plotas ( a*1=a) yra lygus minėtų kvadratų plotų skirtumui, t.y. a^2 – 1=a, tai šis stačiakampis ir yra Gražiausias. Nes pastarosios lygties teigiamas sprendinys yra lygus Ф, t.y. Dieviškajai proporcijai…
Geras tekstinis uždavinys išeitų, tiesa? Jis tiktų ir geometrinės progresijos dėstymui, nes minėti trys plotai ( 1, a, a^2 ) yra iš eilės einantys geometrinės progresijos nariai…
Bet…Ar kas nors tokį uždavinį suformuluos, ar spręs? Ar tiesiog “toliau eis programą”? Nes…
Vieniems “neaišku niekas”, kitiems-“viskas aišku”.
Liūdnas kontrastas…
Uždaviniai buvo ir bus už mus stipresni…Ir negali būti “viskas aišku”. Pažinimo džiaugsmą patirkime…
Burgis, 2016-10-04 10:00:07
Šį kartą 100 proc. pritariu S.Sokolovui… Apie tai parašysiu atskirai.
Sokolovas, 2016-10-04 22:03:04
UŽDAVINIO “GRAŽIAUSIAS TRIKAMPIS” SPRENDIMAS
Kadangi trikampiai ACD ir ABC turi lygius kampus
(< ACD = < ABC ), taip pat ir bendrą kampą
(<CAB ), tai šie trikampiai yra panašūs. Todėl šių trikampių kraštinių, esančių prieš lygius kampus, santykiai yra lygūs.
Pažymėkime x=CA=BD. Tada AB=x+1.
x/ (x + 1) = 1 / x.
Iš čia gauname lygtį x^2 = x + 1.
Šios lygties teigiamas sprendinys ir yra ieškomas ilgis .
Atsakymas: BD=(1 + sqrt5)/2 = Ф.
Taigi, atkarpų BD ir AD=1 santykis lygus Dieviškajai proporcijai !
Pastaba: Atskiru atveju, kai <ACD = < ABC= 36 (laipsniai), < CAB=72 (laipsniai), turime pentagramos ( penkiakampės žvaigždės, sudarytos iš taisyklingojo penkiakampio įstrižainių) “fragmentą”. Nusibrėžkite šią figūrą, ir išvysite nuostabų “peizažą”, bylojantį apie Dieviškosios proporcijos sąlygojantį grožį…
Vilkas Pilkas, 2016-10-07 15:45:01
Gerb. Sokolovai,
klausiate ar geras tekstinis uždavinys išeitų?
Atsakymas yra “ne”. Ir ne dėl to, kad užduotis negraži, tiesiog nedraugauja geometrija su tekstu. Kaip Jūs tikitės perteikti aukso pjūvio grožį tekstu? Pažiūrėkit kaip lakoniškai ir suprantamai pateiktas sprendimas angliškoje vikipedijos versijoje – puslapis Golden_triangle_(mathematics)
Padarykite šio puslapio vertimą i lietuvių kalbą, ir už tai Jums mintyse padėkos tiek “vieni” kuriems „neaišku niekas“, tiek kiti, kuriems „viskas aišku“ (o Jūsų indėlis bus įrašytas gražiom tekstinėm raidėm lietuviškosios vikipedijos istorijoje)