2009 metų lapkričio 19 dieną šioje svetainėje paskelbiau temą „Vidurkių vidurkis nėra vidurkis“. Šiemet savo studentams pažadėjau tai dar kartą parodyti, nes mes dabar mokomės didžiųjų skaičių dėsnius. Pateikiu „Excel“ lapą, iš kurio studentai turėtų suprasti, kaip patyrinėti tą niuansą, kurį jiems per paskaitą papasakojau.
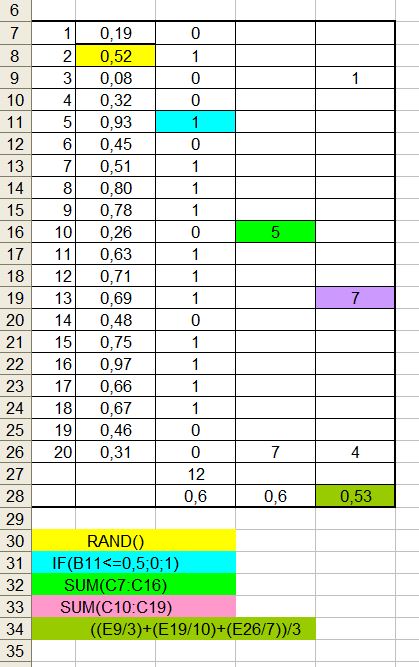
O jums, mieli lankytojai, dar kartą priminsiu, kaip aš moku pagerinti mūsų abiturientų valstybinių egzaminų rezultatus…
*
Tarkime, vienais metais abiturientai kažkodėl laikė tik tris (čia kad būtų mažiau jums skaityti…) valstybinius egzaminus: 70 abiturientų laikė matematikos egzaminą, rezultatų vidurkis 90, 70 abiturientų laikė istorijos egzaminą, rezultatų vidurkis 80, ir 10 abiturientų laikė geografijos egzaminą, rezultatų vidurkis 40 (na, pas mus taip nebūna, bet čia juk pavyzdys…).
Jei aš visuomenei pateikčiau vidurkių vidurkį, tai jis būtų 70 – labai nekoks, tiesa? Bet aš pateiksiu tiesiog vidurkį: (70*90+70*80+10*40)/150=82. O, tai geriau!
*
O kitais metais buvo taip: 70 abiturientų laikė matematikos egzaminą, rezultatų vidurkis 90, 70 abiturientų laikė istorijos egzaminą, rezultatų vidurkis 80, o du abiturientai laikė informatikos egzaminą, rezultatų vidurkis 100.
Visuomenei pateikiu vidurkių vidurkį – 90. Puikus! Jei pateikčiau tik vidurkį, jis būtų (70*90+70*80+2*100)/142=85,2. Kam taip reklamuotis?…
***
Studentų prašyčiau surasti, kada vidurkių vidurkis yra vidurkis, net jei bandymų skaičius nėra didelis. Pateiktoje lentelėje tai matyti. Paklausiu per egzaminą!
Atsakymai
Burgis, 2012-11-24 10:16:06
Ačiū, dėstytojau?…
Mikas, 2012-11-24 15:40:11
vidurkių vidurkis bus vidurkis tada, kai visus egzaminus laikys vienodas kiekis abiturientų. Apskritai su vidurkiais daug fokusų galima prigalvoti 🙂
Ar žinojote, kad Jūs turite daugiau kojų nei vidutinis žmogus? 😀
Arba dar vienas: A mokyklos berniukų pažymių vidurkis didesnis už B mokyklos berniukų vidurkį. A mokyklos mergaičių pažymių vidurkis irgi didesnis už B mokyklos mergaičių vidurkį. Tačiau bendras A mokyklos moksleivių vidurkis mažesnis už B mokyklos moksleivių vidurkį. Kaip taip gali būt?
sqrt, 2012-11-25 11:11:46
O, koks elegantiškas uždavinukas su moksleivių vidurkiais! Reiks kaip nors nepamiršti 🙂
Beje, vidurkiu vidurkis gali būti lygus vidurkiui net jei egzaminus laiko ir skirtingas kiekis abiturientų. Tiesinė neišsigimusi lygtis su n kintamųjų turi dimensijos n-1 poerdvį sprendinių…
Burgis, 2012-11-25 11:37:30
sqrt: „Tiesinė neišsigimusi lygtis su n kintamųjų turi dimensijos n-1 poerdvį sprendinių…“ Taip, Pauliau, gali parašyti tik vienas gabiausių Lietuvos matematikų. Man garbė ir džiaugsmas, kad Jūs čia lankotės. Ačiū!
Lina, 2012-11-25 16:13:22
Šioje svetainėje nesikeikiama, tai paskutinio anekdoto žodžio nerašysiu 🙂 Bet prie vidurkių temos tinka
Kažkokiam kaime vyksta melžėjų kursai. Ten jom aiškina kiek karvės vidutiniškai šieno suėda, kiek pieno duoda ir t.t
Viena melžėja ir klausia:
– O kas tas yra vidutiniškai?
Dėstytojas:
– Na čia yra kai žinom kiek karvės suėda šieno, ir žinom kiek iš viso yra karvių, tada dalinam iš jų skaičiaus suėstą šieną ir žinom kiek vidutiniškai viena karvė suėda šieno.
Melžėja:
– A, aišku, tai jei Marytė turi 2 meilužius, Irena vieną, o aš neturiu, tai vidutiniškai ir aš esu k….!?!!
Ronaldas, 2012-12-06 01:19:23
Būtų galima sužinoti Miko cituoto uždavinio paaiškinimą?
Vis nesiseka sugalvoti, kaip taip išeina.
pijus, 2012-12-28 20:23:56
Ronaldui Miko cituoto uždavinio sprendimas: gali būti pvz A mokykloj mokosi du berniukai ir viena mergaitė, o B – atvirkščiai vienas berniukas ir dvi mergaitės. Tačiau A mokykloj mergaitės vidurkis 10, berniukai nesimokė ir jų vidurkis po 6, o B mokykloje mergaitės gavo po 9, o berniukas – tik 5. Viskas sąlygą atitinka, nes A mokyklos mergaičių vidurkis (10) didesnis už B (9), berniukai irgi atitinka – A mokyklos berniukų vidurkis 6, o B mokyklos 5. Tačiau A mokyklos vidurkis mažesnis už B, nes
(A mokyklos vidurkis – viena mergaitė ir du berniukai) (10+6+6):3=7,33
(B mokyklos vidurkis – dvi mergaitės ir vienas berniukas) (9+9+5):3=7,67
Pats uždavinio ,,kabliukas” yra toks, kad nenurodytas berniukų ir mergaičių skaičius A ir B mokyklose