Ar tu prabundi naktį? Ne? Net dabar, pavasarį, neprabundi?
Tai gal su sveikata negerai?
*
Aš tai prabundu. Ir, žinoma, tuoj kas nors įlenda į galvą. Pavyzdžiui, šiąnakt štai toks elegantiškas uždavinėlis:
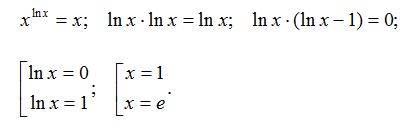
Pripažink – tiesiog mokymo priemonė!
*
Esu pakviestas surengti kelis seminarus matematikos klausimais. Bet gal atšauks? Gal niekam nebereikia tos matematikos? O gal aš dabar tiesiog nepageidaujamas, kaip teroristas Paryžiuje? Pamatysime. Neleis kalbėti apie matematiką – rašysiu pasakas arba eilėraščius.
Taip, tai grasinimas.
Labanakt.
*
Saulė žarą lyg vyną paliejo,
Susisupo šešėliais beržai.
Ką siunti, sutemų karaliene,
Kas nematoma šiąnakt ateis?
Atsakymai
Burgis, 2015-04-22 22:09:35
Vakarinis kokteilis…
Sokolovas, 2015-04-22 22:32:13
UŽDAVINIAI APSIREIŠKIA NORINTIEMS TO…
Dar įdomi nelygybė, gauta, pakeičiant gerb. Burgio pradinėje lygtyje lygybės ženklą ženklu > ( daugiau), t.y.
x laipsniu lnx > x . Ats: ( 0 ; 1) U (e; plius begalybė)
P.S. Aišku, matematikos reikia! Uždaviniai už mus stipresni. Ir jų daugiau nei mūsų. Tad pasidžiaukime, jų didybę pajausdami !
Rasa, 2015-04-22 23:35:50
Pavasarį matematika įgauna keistų pavidalų… Pavasarį viskas dera. Meilė- poezija- matematika…
***
Kai dar nemiegu, sprendžiu, kurios lygtys įdomesnės- gal O. Baliukonės, kai iš nieko (nulio) išgaunama begalybė (pasaulis)? Štai uždavinys:
…Iš nieko sukurti pasaulį. Du vieniši,
Du ieškantys vienas kito gyvens čia
Saulėtą ilgą naktį. Paukščiai
Giedos paveiksle ant sienos. Medis pražys,
Per pusę perskeltas žaibo, dviem šerdimis,
Dangaus pačiam vidury – lauke žvaigždėtam.
Taip žydi akimirką akmenys, žmonės, lietūs
Po laiko amžina širdimi…
***
O gal paprastesnė meilės geometrija?
R. Sternberg’o (“A triangular theory of love”, 1986) trikampio teorija teigia, kad yra trys pagrindiniai meilės komponentai: artimumas, aistra ir atsidavimas. Artimumas – tai atsivėrimas, dalinimasis mintimis ir emocijomis su kitu asmeniu. Aistrą “sudaro” erotinis susidomėjimas ir artimi santykiai. Atsidavimas – tai sprendimas būti su vieninteliu žmogumi ir nekreipti dėmesio į kitus potencialius partnerius.
***
Spalvotų sapnų visiems! 🙂
Temidė, 2015-04-23 09:03:19
Aš 2 žingsnyje būčiau abi puses padalyjęs iš ln(x) ir x=1 pametęs. Bet ko norėt – juk esu aukšto nacionalinio lygio mokslininkas (oficialus eksperto pripažinimas).
Sokolovas, 2015-04-23 09:15:33
NEGALIMA DALINTI IŠ KINTAMOJO, “KAI TO LABAI NORISI”
Temidei:
Tai, deja, dažna klaida. Bet negalima teigti, kad iš viso negalima lygties abiejų pusių dalint iš kintamojo.
Negalima tik tada, kai šis kintamasis dauginamasis yra visuose lygties nariuose. Tada keliam į vieną pusę, ir lygtį pakeičiame vienanare lygtimi.
O , pavyzdžiui, spręsdami lygtį
sinx = cosx,
abi puses dalijame iš cosx. Gauname ekvivalenčią lygtį
tgx=1,
Ir sprendinių neprarandame. Tačiau retas mokinys sugalvos taip padalinti, kol jam nebus “parodyta pirštu”.
O štai klaidinga dalyba yra patraukli ( kai dauginamasis su kintamuoju yra visuose lygties nariuose). Uždraustas vaisius saldus!
petras, 2015-04-23 10:26:34
p. Sokolovai, o kaip matematiškai užrašyt lygties x=x sprendimą ?
Sokolovas, 2015-04-23 10:37:03
SVEIKINAME TAPATYBIŲ GROŽĮ !
Petrui
0x = 0,
x priklauso ( – begalybė; + begalybė)
P.S. Dėkui už įdomų klausimą. Dar pridursiu, jog lygtis, kurios sprendinių aibė yra intervalas ( nebūtinai toks, kaip šiame pavyzdyje), dar yra vadinamos tapatybėmis.
Pvz: arcsinx + arccosx = pi/ 2.
Šios lygties sprendinių aibė [ -1; 1]
Tai yra tapatybė, t.y. lygybė, teisinga su visomis leistinosiomis ( t.y. priklausančiomis minėtai atkarpai) kintamojo x reikšmėmis…
Lygties lnx = lnx sprendinių aibė ( 0; + begalybė),
ir t.t….
petras, 2015-04-23 11:36:10
tada dar vienas prašymas būtų, gal galėtumėte tos antros lygties su arksinusu ir arkosinusu parašyti sprendimą ? (jeigu nėra labai sudėtingas jis)
Burgis, 2015-04-23 12:47:19
Petrui: jei Jūs dar žinotumėte, kad arcsin(pi/6) yra beveik (pi/6)…
Sokolovas, 2015-04-23 13:23:33
Petrui:
Pažymėkime z = arcsinx, z priklauso [- pi/2 ; pi/2 ]
Tuomet x = sinz, x priklauso [ -1; 1 ]
sinz = cos( pi/2 – z), beje, pi/2 – z priklauso [0; pi ]
Todėl cos(pi/2 -z) = x, t.y. pi/2 – z = arccosx.
Iš čia gauname: arcsinx + arccosx = z + pi/2 – z = pi/2
kai x priklauso [ -1; 1].
Sokolovas, 2015-04-23 13:33:36
Gerb. Burgiui:
Taip, iš tikrųjų!
Alternuojančios eilutės
pi/ 6 = 2/3- 2/9 + 2/15- 2/21 + 2/27 – 2/33 +…
dalinės sumos “svyruoja” apie 1/2…
Beje, žmonės turėtų susižavėt štai kuo:
Baigtinė paprastųjų trupmenų ( sveikųjų skaičių santykių) suma yra racionalusis skaičius.
O štai begalinė suma ( aišku, matematiškai tai yra sumos riba…) yra iracionalusis skaičius!
Burgis, 2015-04-23 13:35:48
Sokolovui: Jūs dar nepamiršote, kad čia ne Jūsų svetainė? Kad reikia turėti saiko?
Sokolovas, 2015-04-23 13:35:58
Tiksliai- gali būti iracionalusis skaičius. Turėjau omeny išnagrinėtą atvejį, už kurį dėkoju arktangentui bei jo skleidiniui laipsnine eilute…
Sokolovas, 2015-04-23 13:37:48
Gerb. Burgiui. Aš tik į klausimus atsakiau žmonėms…Be abejo, svetainė Jūsų. Esu dėkingas Jums už galimybę padiskutuot matematikos klausimais…Ir džiaugiuosi, kad žmonės domisi…
qwerty, 2015-04-23 15:15:11
Na bet jūs ir duodat, matematikai, jūsų formulėse nieko nesuprantu.Įdomu, per kiek laiko įsikirsčiau nors kiek?
Random, 2015-04-23 15:21:35
qwerty, jei mokykloj būtų išmokę pagrindus – nebūtų problemų suprast. Vakar paaiškėjo, kad net VU studentai neturi nuovokos kas yra dalyba… Ką jau kalbėt apie logoritmą, diskriminantą, trigonometrines funkcijas… Taip, atpažint ženkliuką / * + – gal ir išmoko, bet nieko daugiau, o viskas, ko dabar nesupranti, ir susideda iš pagrindų.
Tai kaip čia pasakius, kad gerai įsikirstum – reiktų nuo visai kitų dalykų pradėt, bet tai nėra nieko blogo 🙂
Rasa, 2015-04-23 15:29:23
O, Qwerčius sugrįžo! 🙂 Jau maniau, kad panemuniais žibutes tik rankioja ir kompą su matematika pamiršo 🙂
Barbaras, 2015-04-23 18:14:01
Ji kaip zydinti pieva. Kaip migla paupy saulei kylant…
Laume. Rasa…
………………………………
…Ak.. jeigu žinotum,
kad visi tavo žodžiai yra užkalbėjimai
kad jie tyliai veikia
kol tu miegi, eini,
kol nesurandi sau vietos,
keiti gyvenimus..
Ar vis dar rašytum apie tai?
apie skausmą ir ilgesį
apie stingdantį nerimą
ir tą tautų nelaukiamąją ?
.
Turbūt…
nes kitaip tiesiog neišeina
nes ir neužrašyti jie pildosi
lyg pranašystės..
Gali nuo jų bėgti, gali nutylėti,
bet jie čia
Visa – ir gera ir bloga… (Glesumele)
Jonas, 2015-04-23 19:43:19
Išėjau aš vieną vakarą į gatvę
Gatvę juodą, gatvę purviną ir šlykščią.
Nieks nelydi, nesutinka, nepasiūlo
Apliūdėti mano laimę vakarykščią.
Buvo rūkas. Drėgnos tvoros, kreivos lūšnos.
Kažkas verkė, kažkoks balsas toly spiegė…
O rūke kaip žiburiai pakibę žodžiai:
Tavo laimė ir beprasmė, ir bejėgė.
Kažkur ore šniokštė šakos, staugė vielos,
Vielos staugė, vėjas daužė seną skardą.
Kažkas šaukia. Klausia vardo? Ne tai monai
Pamiršau aš vakar dieną savo vardą.
Nesustojau, nepatyriau, kas ten šaukia,
Tik ėjau per gatvę juodą, gatvę šlykščią
Į tą naktį, į tą rūką, į tą vėją
Apliūdėti savo laimę vakarykščią.
V,M.P
qwerty, 2015-04-23 20:02:02
Sveika, Rasa, Adefagija,niekur nebuvau išėjęs.Skaitau jus)
Margos paraštės, 2015-04-23 21:02:00
Jėzau ir Marija! Ar jūs negalit tų formulių paversti poetui suprantama kalba?! Kaip man suprasti, kas ten prikeverzota? 🙂
petras, 2015-04-24 08:26:36
Neteko sutikt šioj svetainėj nei Jėzaus nei Marijos, tai kaži ar jie tau ką pavers.
Violeta, 2015-04-24 10:23:54
Barbarai, gal žinote, kas rašo Glesumėlės slapyvardžiu – seniai jau jos posmus skaitau
Barbaras, 2015-04-24 16:34:03
Violetai: Gintare Stankute
Violeta, 2015-04-25 20:21:52
Ačiū, Barbarai 🙂
ST, 2015-04-28 16:02:55
Matematinės poezijos pavyzdys:
Tarkim, kad žemė apvali ir jos spindulys R yra 6371100 metrų (pagal Vikipediją).
Jei žemę apjuostume virve ir norėtume tą virvę pakelti į 1 metro aukštį, tai kokio ilgio virvės gabalą reikėtų pridurti?
Nuojauta sako, kad virvės reikės nemažai.
Paskaičiuokim…
Apskritimo ilgis yra 2*π*R. O kai spindulys padidintas vienu metru, tai 2*π*(R+1).
Paskaičiuojam skirtumą: 2*π*(R+1) – 2*π*R = 2*π.
Laikant, kad π=3,14, gaunam kad reikės apie 6,28 metro papildomo gabaliuko virvės ir aplink žemę apjuostą virvę galėsim kilstelėti į 1 metro aukštį 🙂
Ir dar – nesvarbu, kas su virve buvo apjuostas, ar žemė, ar krepšinio kamuolys, spindulį padidinus vienus metru prireiks papildomai apie 6,18 metrų virvės gabalo.
O kaip su apskritimo, kurį ta virvė apjuosia, plotu?
Žemės apjuosimo atveju, pailginus virvę 6,28 metro, plotas, kurį su ta virve galima apjuosti, padidėja apie 40010511,14 kvadratinių metrų (apie 40 kvadratinių kilometrų). Vau!
Štai tokia matematinė poezija – nebent skaičiavimuose yra klaidų 🙂
Sokolovas, 2015-04-28 16:50:06
ST:
Viskas gerai. Tik plotas ne apskritimo, o skritulio…
Sokolovas, 2015-05-17 15:59:07
TURININGAM LAISVALAIKIUI
Skaičius a tenkina lygybę:
( a – 30)(a + 30) = 2a + 107
Apskaičiuokite:
a(a – 32)(a + 32) + 13a + 1.
Juozas P., 2016-07-12 14:10:05
Atsiprašau, kad įpėdinu su savo trigrašiu, gal banaliu, bet gal vis tik tinkančiu temos pavadinimui…
Музыка числа Пи
https://www.youtube.com/watch?v=IOMkTGZ6GuU&list=RDIOMkTGZ6GuU