Savaitgalį mėgavomės anūkėlėmis, neturėjau laiko komentuoti. Apsidžiaugiau radęs netikėtai daug komentarų parabolės tema. O juk atrodo, kad vasarą tai taip nuobodu…
*
Bet jei jums nenuobodu, tai ir aš šiek tiek prisidėsiu. Laiko vis dar turiu nedaug, todėl atsiprašau už siaubingai nevykusius brėžinėlius… Bet man svarbu pakomentuoti keletą klasikinių dalykų.
*
- Yra teigiančių, kad vos pasukus parabolę, vertikali tiesė ją kirs dviejuose taškuose. Matematikos klasika liepia klausti: ar tai tinka bet kuriai parabolei? Ar parabolės parametrai visai neturi reikšmės? Taip gali būti, bet šiuo atveju tuo sunku patikėti, pažvelgus į paveikslėlius Nr. 2 ir Nr. 3:
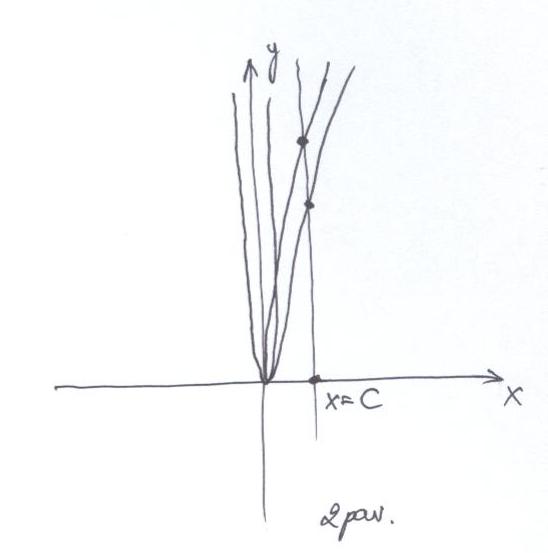
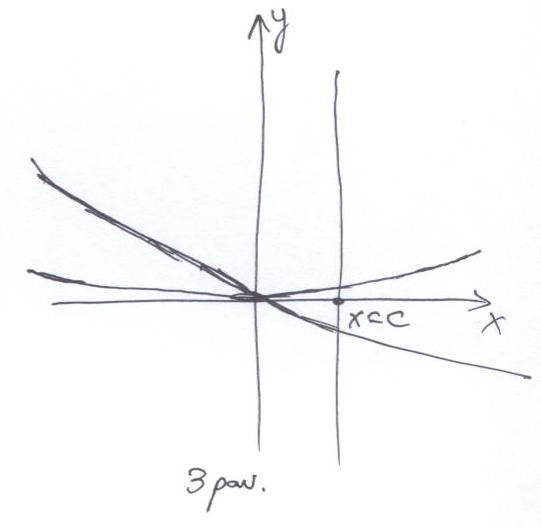
Taigi vertėtų panagrinėti, kiek čia svarbus parabolės „statumas“. O nuo ko jis priklauso? Nuo židinio ir direktrisės.
-
Kitas matematikos klasikos principas: arba tas kampas, kai tiesė kerta parabolę tik viename taške, yra ribinis, išskirtinis (šiuo atveju – nulis laipsnių), arba sprendinys yra kažkoks „lūžio taškas“ (sukant nuo 0 iki 90 laipsnių). Tada vėl galimi tik du atvejai: tas „lūžio taškas“ visoms parabolėms yra tas pats (nepanašu!?); tas taškas priklauso nuo parabolės parametrų.
-
Kalbos kalbomis, bet reikia įrodyti! Tai vėl matematikos klasika. Įrodymas gana paprastas: reikia ieškoti parabolės ir tiesės susikirtimo taško (taškų), o tai reiškia, kad reikia spręsti parabolę ir tiesę aprašančių lygčių sistemą. Kol parabolė nepasukta, sistemą, žinoma, galima išspręsti mintinai! O kai parabolė pasukta… o, mes pirmiausia turime sudaryti pasuktos parabolės lygtį! Bet tam reikia prisiminti, kas ta parabolė!
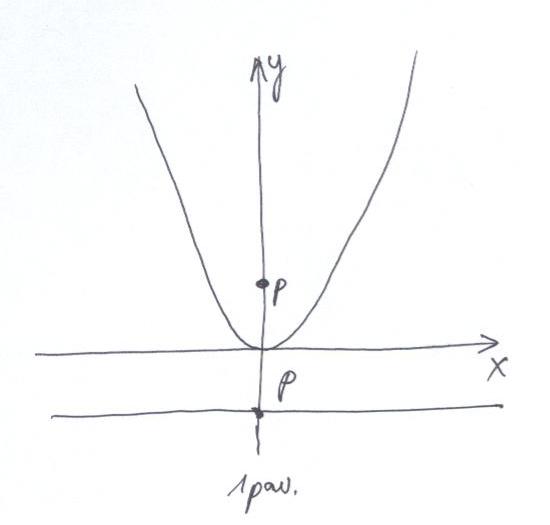
Grįžtame į pradžią (1 pav.). Parabolė yra kreivė, kurios bet kurio taško (pažymėkite M(x;y)) atstumas iki tiesės, vadinamos direktrise, lygus atstumui iki taško, vadinamo židiniu. 1 pav. matote ir židinį, ir direktrisę. Nesunkiai (jei mokate Pitagoro teoremą) rasite, kad parabolės y=x^2 atstumas p=1/4.
- Man labai patinka matematikos klasikos principas, kurį vadinu „pratęskime iki begalybės“. Šiuo atveju išnagrinėčiau dvi pasuktas paraboles: vienos p pasirinkčiau 0,001, kitos 1000. Tai, žinoma, ne begalybės, bet pakaks skirtumui pastebėti…
***
Taigi dabar pasukite parabolę 45 laipsnių kampu ir pasikankinkite… :-). Po to pakeiskite parametrą p ir vėl pasikankinkite… :-).
Atsakymai
Burgis, 2011-06-21 10:01:40
Niekas nenori kankintis? Provokuoju. Patikrinkite, gal tai ir yra 45 laipsniu pasuktos parabolės lygtis:
(x-y)^2 – 4sqrt(2)p(x+y) = 0.
Jei taip, tai daug kas paaiškėtų…
Paulius, 2011-06-21 17:55:02
Kankinausi, bet nelabai kas paaiškėjo… Radau, jog a laipsnių (0<a<90) pasuktos parabolės lygtis:
(x-y)^2 – p( 6ysina+6xcosa+2ycosa+2xsina). Tai bent kiek pravartu?
Burgis, 2011-06-21 18:46:25
Pauliui: šaunuolis! 100 balų! Pastebėkite, kad iš Jūsų lygties, kai kampas yra 45 laipsniai ir x=0, gauname tuos pačius sprendinius, kaip ir iš manosios. O tai ir yra uždavinio raktas!
Burgis, 2011-06-22 20:48:17
Niekas nebesikankina, tai norėčiau diskusiją užbaigti ir paskirti Pauliui prizą. Bet… Paulius turėtų įrodyti, kad iš jo lygties, kai a=0 ir kai a=90 laipsnių, gaunamos mano aukščiau pateiktos parabolių lygtys. Tai dar vienas matematikos klasikos principas: iš bendrybės turi būti gaunama atskirybė.
*
O dabar patvirtinkite arba paneikite mano sprendimą.
Ankstesnėje temoje kažkuris įžvalgus skaitytojas pasiūlė: sukime ne parabolę, o ją kertančią tiesę. Tai aš ir siūlau: kirskime laaaabai išsiskleidusią parabolę y=0,001x^2 laaaaabai mažai pasvirusia tiese y=-1000x. Gal nesusikirs dviejuose taškuose? Susikirs! 0,001x^2=-1000x; x1=0; x2=-1000000. Toli toli – bet susikirs. Tai netiesioginis įrodymas, kad parabolė neturi asimptočių, tiesa?
Bet gal čia klasta?
*
Po trijų dienų temą perkelsiu į sandėliuką. Laukiu Pauliaus laiško su patikslinimais ir su trumpu prisistatymu: kas, iš kur, kokio amžiaus, profesijos, kur siųsti prizą (jei siųsiu…).
petras, 2011-06-23 09:04:42
Na, Pauliau, pavaryk ! žmonės tiki tavim 😀
Paulius, 2011-06-23 18:00:14
Kovoju, bet sunkiai judu iš mirties taško. Pavyko tik pastebėti, jog buvau užrašęs klaidingą pasuktos parabolės lygtį. Tikroji – gerokai bjauresnė:
(ysina-xcosa)^2 – 4p(ysina+xcosa) + pcos2a(p-2ysina+2xcosa)=0. Tačiau ją radau, tardamas, jog a nelygu 0 arba 90. Tad lyg ir negalėčiau statyti šių a reikšmių į lygtį. Visgi jei pabandau, gaunu (x-p)^2=0 arba (y-p)^2=0. Gal kažkas panašaus į direktrisės lygtis? Nežinau, kaip čia išsisukti… Bet kuriuo atveju, nerandu, kuo mum svarbi p reikšmė. Be to, gal galėtumėte paaiškinti, ką reikia patvirtinti arba paneigti Jūsų pateiktame sprendime? Nelabai suprantu, apie ką ten mintis sukas, bet galbūt toji klasta susijus su tuo, jog pasukta tiesė x=c būtų formos kx+b t.y. neitų per tašką (0;0)?
Laurynas, 2011-06-23 20:15:10
(Ne sprendimas, bet komentaras): įsivaizduokim, kad kreivės y=x^2 ir y=ax+b nubrėžtos ant elastingos baigtinės kvadratinės plokštumos. Jei tempsime plokštumos šonus vieną nuo kito arba spausime vieną kito link, o viršų ir apačią palikstime vietoje, tai gausime bet kokią norimą parabolę y=kx^2. Gan akivaizdu, kad tiesė išlikt tiese, parabolė išlikt parabole, ir jų susikirtimų skaičius išliks tas pats. Vienintelis parametras, kuris keisis tai kampai. Tad iš esmės, modelis bus tas pats (žr. anstesnį komentarą): sukant parabolę pagal laikrodžio rodyklę kampu 0<s<pi/2, tiesė x=c kirs ją dukart. Sukant parabolę prieš laikrodžio rodyklę, kažkokiu mažu kampu, tiesė ir parabolė turės du bendrus taškus.
Na, o matematiškai tokią plokštumos operaciją galima užrašyti bitiesine transformacija f(x,y)=(kx,y). Norint, galima viską susiskaičiuoti tiksliai.