Atsiprašau, kitiems tai nebus įdomu, net negaliu nurimti – mano studentai turi išmokti spręsti tokį paprastą uždavinį! Po vakarykščio bandymo su gyvais žmonėmis privalau parodyti, kad sprendimas gali būti paprastas ir aiškus.
Strypas perpjautas dviejose atsitiktinai pasirinktose vietose. Kokia tikimybė (įvykio T), kad iš gautų strypelių galima sudaryti trikampį?**
*
Tarkime, kad strypo ilgis yra A, o po supjaustymo gautų dalių ilgiai yra x, y ir z.
Akivaizdu, kad turi būti teisinga lygybė x+y+z=A. Tai plokštumos lygtis! Vadinasi, visų galimų rezultatų aibė gali būti parodyta trikampiu pirmame oktante.
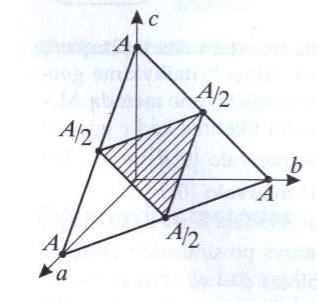
Trikampį iš strypelių galėsime sudaryti, jei bus teisingos nelygybės: x<y+z, y<x+z, z<x+y. Ką duoda plokštumos lygtis kartu su, pavyzdžiui, paskutiniąja nelygybe? Užrašykite sistemą ir gausite: z=A-(x+y), z<A-z, z<A/2.
Analogiškai gausime x<A/2, y<A/2. Šios trys nelygybės apibrėžia užbrūkšniuotą aibę. Tos aibės (trikampio) plotas yra ketvirtis didžiuojo trikampio ploto. Atsakymas: P(T) = 1/4.
*
Išvada: neskubėkite patikėti, kad jus moko nesuprantamų dalykų!
P.S. 1) Paveikslėlį paėmiau iš savo „Niekam tikusios matematikos mokymosi knygos“, jis šiek tiek neatitinka teksto. 2) Įrodyme palieku klaidelę! Raskite ją.
Atsakymai
Burgis, 2011-11-10 11:38:41
Įvertinkite mano švietėjiškas pastangas…
Palaidas, 2011-11-11 12:44:16
Panašu, kad tikimybė tokia, bet užbrūkšniuotas trikampis ne ten įbrėztas. Jo viršūnės turėtų remtis į ašis ties A/2.
ST, 2011-11-11 12:52:13
“Prisikabinčiau” nebent prie teiginio “Šios trys nelygybės apibrėžia užbrūkšniuotą aibę”.
Tos nelygybės (x<A/2, y<A/2, z0, y>0, z>0) apibrėžia kubą. O ta užtušuota sritis yra kubo ir plokštumos (x+y+z=A) sankirta.
ST, 2011-11-11 12:54:30
Iš komentaro dingo dvi nelygybės z>0 ir z<A/2.
ST, 2011-11-11 12:57:22
Tiksliau, dingo x>0 ir z<A/2 🙂
Burgis, 2011-11-11 20:32:13
Ne, kol kas jūsų nurodyti dalykai nėra esminiai… Nebūtina rašyti to, kas savaime aišku, pavyzdžiui, x>0.
nuoba, 2011-11-11 20:59:22
Gal ne ten užbrėžta A/2 taškai. Geriau tiktų ant vektorių a,b,c (t.y x,y,z)?
Pranas, 2011-11-14 22:33:09
Keista. Man atrodo, kad idėja gera, o ir rezultatas korektiškas-elegantiškas. Liksiu nustebęs, jei čia trūksta kažko svarbaus.
Vainius, 2011-11-14 23:44:36
Neparodyta, kad kiekvieno taško trikampyje tikimybės tankis vienodas?