Dirbu su Statybos ir architektūros fakulteto studentais. Žinau, kaip nieko nenusimanau statybose, todėl stengiuosi pasimokyti iš tų, kurių pašaukimas – statyba.
*
Šiandien pasiūliau tokį uždavinį.
Turime vieno kvadratinio decimetro ploto kvadratinę auksinę plokštelę. Norime iš jos pasigaminti didžiausio tūrio uždarą gretasienio formos dėžutę. Kokią išklotinės iškarpą pasirinktumėte?
*
Susidomėjau, kai studentas nuėjo prie lentos ir pasiūlė „įstrižą“ iškarpą. Niekada nebuvau pagalvojęs, kad gal taip gausime talpesnę dėžutę, negu iš „stačios“ iškarpos. Nutariau išspręsti tą uždavinį.
*
Atsiprašau, nemoku braižyti nei kompiuteriu, nei ranka, bet gal suprasite…
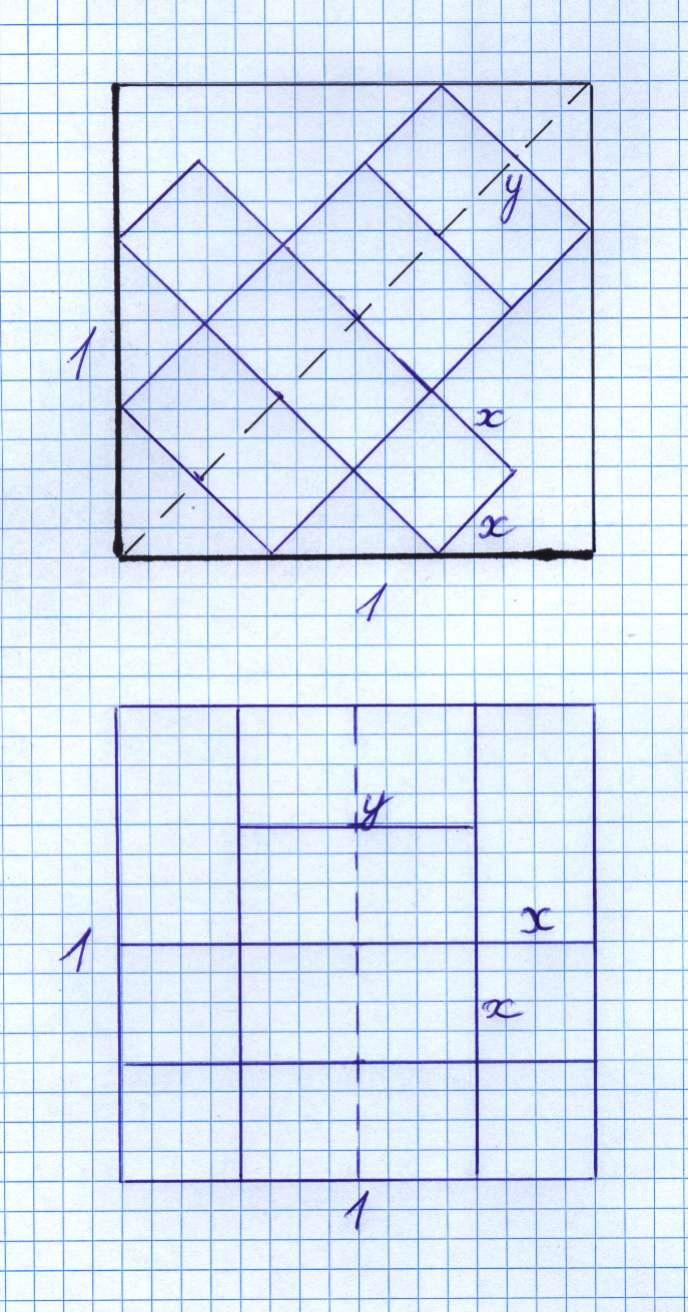
Pirmasis atvejis.
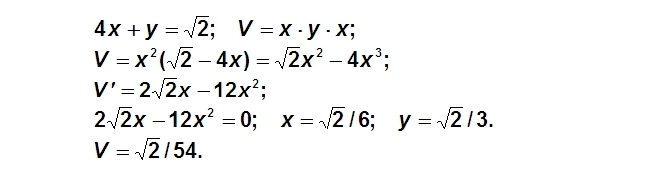
Antrasis atvejis.

Pastebėkite, kad pirmuoju atveju „važiavome aplink“, panaudojome išvestinę tik norėdami garantuoti, kad gautasis tūris yra maksimalus, o šiaip tas tūris buvo aiškus be jokios išvestinės. Pastebėkime, kad taip bandant padaryti kubo formos dėžutę (šiaip jau didžiausio tūrio dėžutę, kurios paviršiaus plotas nekeistinas…), gautume:
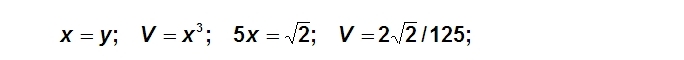
Šis tūris yra mažesnis už anksčiau gautąjį! O didžiausias tūris yra 1/32. Taigi, statybininkai…
**
Papildymas 2011 11 29.
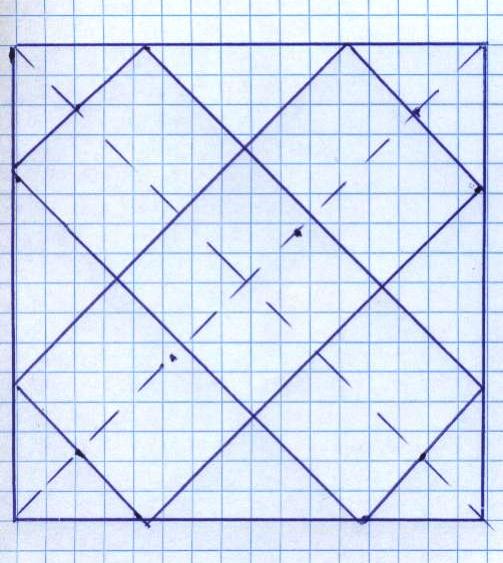
O štai ir originalus sprendimas, kurį pasiūlė šios svetainės lankytoja (lankytojas?). Nors „dangtelis“ keistokas, bet už tai tūris – beveik pusantro karto (šaknis iš 2) didesnis už 1/32! Įdomu, gal galima dar?…
***
P.S. Nubraižiau visai kreivai, nes jūs vis tiek visai nevertinate mano darbo… Kas čia per reitingai?! O man vis tiek atrodo, kad tokia diskusija naudinga.
Atsakymai
Burgis, 2011-11-28 16:11:40
Na, pagirkite už darbą…
Giedrius, 2011-11-28 16:22:38
Baisu! Jokių “auksinių tualetų”, jokių “važiavimų aplink”…Ar mums reikia tokių statybininkų? Anot drg. Stalino, “…a ni slishkom li vy umny tov. Zhiukov (…Burgis)?
įdomu, 2011-11-28 18:31:31
Hm, man keistas pasirinkimas kad plotis ir aukštis vienodi (lygūs x). Pvz., jeigu ilgis y=0,8, plotis x=0,4, o aukštis z=0,1, tai gaunasi tūris V=0,032=1/31,25 > 1/32=0,03125. Gaunasi didesnis tūris.
įdomu, 2011-11-28 18:53:00
x=1/3; y=2/3; z=1/6; V=1/24 🙂
įdomu, 2011-11-28 18:54:12
atsiprašau, t.y. V=1/27
Burgis, 2011-11-28 18:56:11
įdomu: puiku! Aš ir neteigiu, kad mano pateikti trys variantai yra geriausi! Aš palyginau tris, o dabar erdvė visiems keisčiausiems variantams…
P.S. „įdomu“, jei Jūs – mano studentas – galime derėtis…
agni, 2011-11-28 20:32:49
nesu tikra, ar nelaužau Jūsų žaidimo taisyklių, bet mano dėžutė būtų įpiešta įstrižai, dėžutės pagrindas būtų pačiame plokštelės viduryje, o viršutinis dangtelis būtų sudarytas iš keturių stačiųjų trikampių, kurie susidarytų plokštelės kampuose.
jei gerai suskaičiavau, tai tūris būtų šaknis(2) / 32
Burgis, 2011-11-28 20:39:03
agni: mes sutarėme, kad dėžutės dalių negalima lituoti, visą dėžutę reikia iškart sulankstyti iš iškarpos.
agni, 2011-11-28 20:48:48
na, mano iškarpa vis dar yra viena detalė, jos lituoti nereikia. Tik ją sulanksčius bus plokštelių sudūrimas ne ties kraštinėmis, o sienelės viduryje.
Burgis, 2011-11-28 21:43:40
agni: nesupratau, nes noriu miego… Rytoj gal suprasiu.
įdomu, 2011-11-29 00:32:22
Agni variantas puikus. Šios temos pirmajame paveiksliuke beveik ir yra tas variantas: gretasienio pagrindas – pirmo paveiksliuko centre nupieštas kvadratas kurio kraštinė šaknis(2)/3. Gretasienio aukštis – šaknis(2)/6. Tik tūris gaunasi dar didesnis nei užrašė: šaknis(2)/27.
Burgis, 2011-11-29 11:42:56
agni: supratau ir dėkoju! (Žr. papildymą). Daugiau šia tema nediskutuosiu, nes oponentai kandžiojasi… Kodėl kandžiojasi? Nesupratau ir jau niekada nesuprasiu…