Vienas iš įdomesnių uždavinių, kuriuos esu matęs iš elementarios geometrijos: rasti trikampio plotą, kai žinomos dvi kraštinės, lygios 3 ir 7 ir pusiaukraštinė tarp jų, lygi 4. Galvojau, bet taip ir nesugalvojau, kaip šį uždavinį išspręsti be Herono formulės.
miklis
***
Jūs nežinote, kas yra komentatorius „miklis“ o aš žinau. Tai labai gabus ir smalsus kadenciją baigęs KTU gimnazistas.
Pamatęs jo uždavinį komentare, negaliu iškęsti ir negaliu neparodyti klasikinio sprendimo be Herono formulės. Palyginimui – ir su Herono formule.
Žinoma, be Herono formulės „skalbimo padaugėja“, bet koks gėris, jei jos neprisimeni!
Sprendimo nekomentuosiu. Smalsieji supras, o kitiems jo ir nereikia…
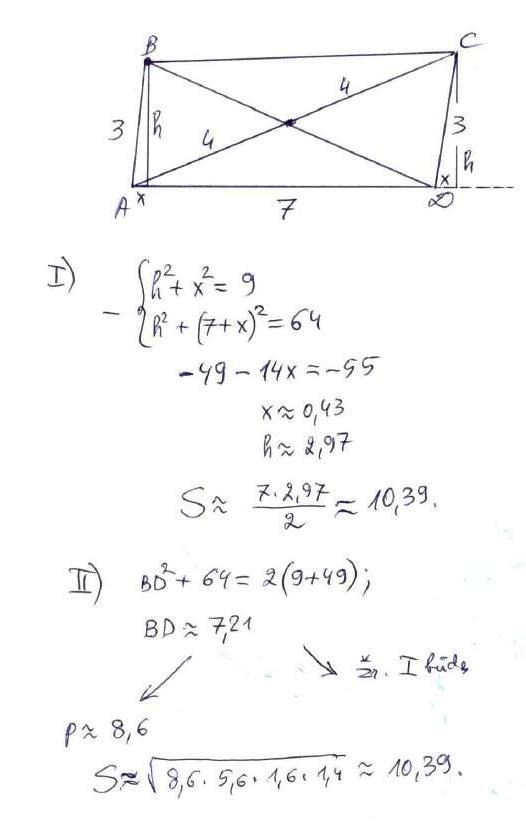
Atsakymai
Burgis, 2015-02-13 20:17:30
Kas mudviem su „mikliu“ padėkos, moksleiviai?…
Sokolovas, 2015-02-13 21:35:55
GRAŽUS UŽDAVINYS! IR…DAR VIENAS BŪDAS
Taikydami kosinusų teoremą, gausime, jog kampas BAC (tarp kraštinės AB ir pusiaukraštinės) yra lygus 60 laipsnių. Todėl trikampio AMB (kur AM-pusiaukraštinė) plotas lengvai skaičiuojamas:
(1/2)AB AM sin60=3šaknys iš 3.
Kadangi pusiaukraštinė dalija trikampį į du lygiapločius trikampius, tai atsakymas 6 šaknys iš 3
P.S. Kampo BAC skaičiavimas tokiame trikampyje ( ats: 60 laipsnių )- irgi įdomus uždavinys…
miklis, 2015-02-14 00:15:38
Oi, Jūs vis mane giriate, kai tik paminite. Net dažnai pasijaučiu, kad nenusipelnau gyrimo.
Gediminas, 2015-02-14 02:59:06
Koks elegantiškas sprendimas!
Burgis, 2015-02-14 08:00:23
Dėl sprendimų:
-
Kadangi trikampių ABD ir ABC plotai lygūs, tai trikampiui ABC (kraštinės: 3, 7, 8) iškart galima taikyti Herono formulę: sqrt(9*6*2*1)=6*sqrt(3), bet mes juk nenorime Herono, tiesa?…
-
Labai nemėgstu uždavinių, kuriuose „paaiškėja“, kad kuris nors kampas yra „gražus“: 30, 45, 60 ir pan. laipsnių. Gyvenime taip nebūna, todėl mėgstu tik universalius sprendimo metodus!
Sokolovas, 2015-02-14 09:05:25
“GRAŽIAUSIEJI KAMPAI”- 18, 36, 54, 72 LAIPSNIAI…
Tik jie “pamiršti”, apie juos “visi tyli”.
Pentagramos ( ( gimsta, vos tik nusibrėžiame taisyklingojo penkiakampio įstrižaines) kampas 36 laipsniai, joje esančių tam tikrų atkarpų ilgių santykis
Г=(sqrt(5)+1)/2 yra įžymusis AUKSINIS PJŪVIS (Dieviškoji proporcija)…
Beje, sin18=1/(2Г), cos36=Г/2
Yra ir paprastesnių “gražių” figūrų. Pavyzdžiui, trapecija ABCD, kurioje AB=BC=CD, AC=AD. Jos smailusis kampas 72 laipsniai, pagrindų ilgių AD ir BC santykis- vėl Auksinis pjūvis Г.
Beje, ši “gražioji trapecija” gan gražiai “dalyvauja” ir anksčiai minėtoje pentagramoje…
Tuo tarpu nežingeidūs žmonės labai dažnai sako, esą “sqrt(5) yra negražus skaičius”. Nesuvokia jie grožio…:)
Sokolovas, 2015-02-15 12:08:21
DAR ĮDOMUS UŽDAVINYS:
Apskaičiuokite trikampio plotą, kai yra žinomi trijų pusiaukraštinių ilgiai.
petras, 2015-02-15 17:40:03
p. Sokolovai, o tai jums pačių figūrų vaizdas gražus, ar jų skaitinė išraiška ?
Sokolovas, 2015-02-15 19:13:40
GROŽIS REIKALAUJA TĘSINIO IR DĖSNINGUMŲ PAŽINIMO
Gerb. Petrui.
Žinote, o tai yra susiję, neatskiriami dalykai! Kai kalbame apie “gražius santykius” figūrose ( minėjau anksčiau), minime “Dieviškąją proporciją”, t.y. skaičių 1/sin18 . O jis, savo ruožtu, “dalyvauja” įžymiosios Fibonačio sekos ( 1, 1, 2, 3, 5, 8, 13…) n-jo nario formulėje, kuri kur kas sudėtingesnė, nei pati Fibonačio seka. Fibonačio sekos dėsningumas įžvelgiamas iš karto, reikia tik pastabumo. O tikrasis grožis , t.y. apibendrinanti formulė, reikalauja “tęsinio”- kur kas gilesnių matematikos žinių.
Paprasta ir išvaizdi trapecija ABCD, kurioje AB=BC=CD. Bene kiekvienas paskaičiuotų jos kampus. O jei pratęstume…Tai ( dėkui trikampių panašumui! ) galime apskaičiuot “nelentelinio” kampo 18 laipsnių sinuso tiksliąją reikšmę!
Dievinu uždavinius, kurie ne iš karto “pasiduoda”. Nesakau, kad “moku”, ar “išmoksiu” spręst. Tik dėkoju likimui už tai, kas ( kartais) apsireiškia man…
Ir todėl..Sveikinu uždavinius, kurių greit negaliu išspręst. Žinote kodėl? Nes vėliau iš tokių uždavinių gimsta ištisos plejados kitų uždavinių, jų susisteminimų, sprendimo metodų…
Kiek grožio yra TĄSOJE, ir pats grožis, tąsos kildinamas, nepaliaujamai reikalauja TĘSINIO.
Prisiminkime kitas “įžymybes”- skaičius “pi” ir e. Ilgai ieškota ryšio tarp jų. Ir tik kompleksiniai skaičiai “sutuokė” juos ( dėkui Oilerio formulei)…
Grožis, tęsinio reikalaujantis. O šio grožio daugiapakopė struktūra taipogi žavi! Kad ir ką matematikoje bepaimtume, yra taip: Pirmoji pažintis, gilinimasis, išplėtimas, sąsajos, dėsningumų pažinimas!
Greta, 2015-02-19 23:44:18
Ir vėl aš čia. Nebuvau užsukusi gal porą savaičių. Žiūriu, uždavinių abiturientams įdėjote. Taip gaila, kad neužbėgau ir nepabandžiau išspręsti, kol dar nebuvo atsakymai įdėti. Eh, nežinojau tiesiog.
Ir vėl aš čia. Ir vėl man kyla noras pagirti, pasakyti šį tą gražaus. Viduje – begalinė pagarba Jums (nors ne paslaptis – nesame pažįstami). Labai norėčiau tokio matematikos mokytojo, koks esate Jūs. Manau, ir egzaminą laikyčiau tada, ir gerai jį išlaikyčiau. Nes man atrodo, kad kiekvienam dalykui, mokslo ar meno sričiai reikia meilės. Deja, ne kiekvienas mokytojas pakankamai jos turi.
Sakysite – tinginio pasiteisinimas? Galbūt. Bet tinginys laisvai kalba keturiomis kalbomis. Tinginys tyliai, bet ištvermingai ir nepaliaujamai (dieną – naktį) ieško rėmėjų savo svajonių projekto įgyvendinimui. O didžiausias paradoksas – tinginys ilgą laiką buvo rajono matematikos olimpiadų laimėtojas. Būtent – matematikos. Būtų kas pasakęs tada, kad nelaikysiu matematikos egzamino, būčiau pirštą prie smilkinio pasukiojusi. Bet štai pasikeitė mokykla, pasikeitė mokytojai. Meilė prapuolė. Skaičiuoju paskutines 100 dienų ir suprantu – nieko jau nepakeisiu. Tik liūdna šiek tiek. Kaip bet kurią meilę palaidojus. Lyg ir jauti, kad pats kaltas. Tuo pat metu lyg ir supranti, kad meilė – abipusis ryšys, vienas tvirtovių nepastatysi.
Atsiprašau, užsivedžiau poetizuoti. Tarsi koks velnias už liežuvio trauktų. Tiesa, atrodo, kol kas mažiau nusidedu nei gerb. Sokolovas su savo neperskaitomo ilgumo komentarais (nieko asmeniško, tikrai!). Gal man dar bus atleista, o aš pasistengsiu, per dažnai neįkyrėsiu.
Galiausiai, vis tiek norėčiau tokio matematikos mokytojo!
Burgis, 2015-02-20 06:54:47
Gretai: ačiū, ačiū! Jūs taip gražiai rašote, kad matematika Jums bus vieni niekai!
Ruta, 2016-01-28 00:04:44
Miklio brėžinyje lygiagretainio įstrižaine, kurios ilgis 8 pasirinkta ilgesnė įstrižainė.
O jeigu pasirenki jog tai trumpesnė = 8?
Tuomet gaunasi neigiamas x.
Kaip tuomet matematiškai teisingai išsisukama?
Vieną paaiškinimo variantą turiu. Įdomu būtų išgirsti kitų nuomones.