Reikia mokytis matematikos, reikia!
Nes kitaip visai negalėtumėte paskaityti knygos, kurią skaito milijonai žmonių.

Aš ją skaitau lėtai… Dėl trijų priežasčių: 1) vasara, o tokios knygos labiau tinka rudeniui ir žiemai; 2) to Nobelio premijos laureato žodynas gerokai virš mano anglų kalbos viršūnių; 3) čia yra užduočių, kurių mintinai negaliu atlikti.
*
Sakyčiau, tai matematinės psichologijos knyga. Žinoma, čia yra jau matytų, žinomų dalykų, bet vis tiek man smalsu, kaip mano psichologija man trukdo suprasti, kad abi horizontalios linijos yra vienodo ilgio, visos žmogeliukų figūros yra vienodo dydžio…
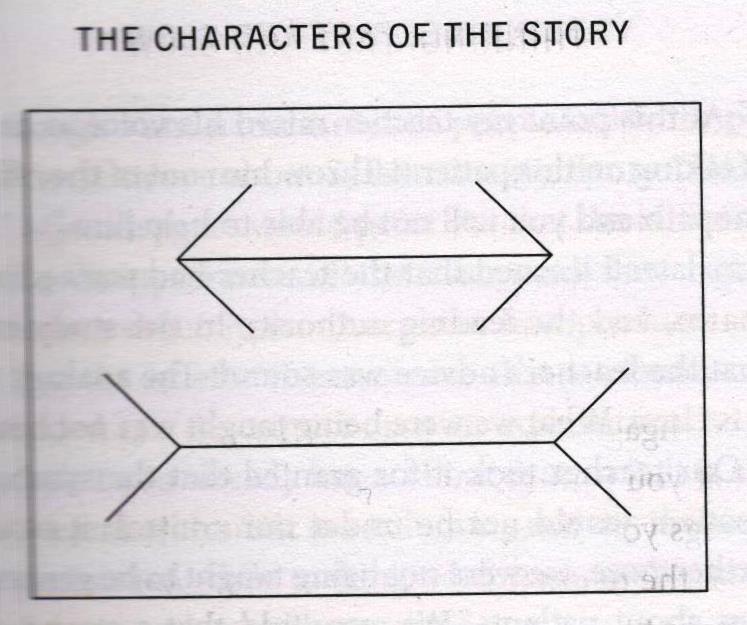

O dabar – du tikimybių teorijos uždaviniai. Būtinai juos pateiksiu studentams, jei tik man leis dėstyti…
Pirmąjį išsprendžiau tik popieriuje, gulint prie baseino karštyje galva atsisakė dirbti…

Antrąjį uždavinį pateikiu su savo modifikacijomis – kad būtų sunkiau…
Keturios lošimo kauliuko sienelės nudažytos raudonai, dvi – geltonai. Kuri seka, mėtant šį kauliuką, labiausiai tikėtina, o kuri – mažiausiai tikėtina?
G R G G G
R G R G G G
R G R G G R R
Nei Bernulio, nei kitų formulių prašyčiau netaikyti! Knygoje nėra nė vieno sprendimo, nė vienos formulės, todėl ji – bestseleris.
Atsakymai
Burgis, 2013-08-06 09:59:46
Aš juk dirbu?…
Burgis, 2013-08-06 10:56:30
P.S. Uždavinių sprendimus čia pateiksiu po savaitės…
Petras N., 2013-08-06 11:00:00
Pirmą, mintinai:
Jei mieste, paprastumo dėlei, yra 100 mašinų (85 žalios, ir 15 mėlynų), tai tas liudininksa, kiekvieną iš jų pamatęs, 17 žalių mašinų įvardins kaip mėlynas (20% klaidos), ir 12 mėlynų mašinų įvardins kaip mėlynas (80% sėkmė). Vadinasi, iš visų 29 (statistinių) mašinų, kurias liudininkas įvardintų kaip mėlynas, iš tikrųjų mėlynos bus tik 12, kas yra ~41%.
Efektas gaunasi toks todėl, kad klaidos ribos yra didesnės už mašinų populiacijos pasiskirstymą – vadinamas “false positive” efektu.
Panašus atvejis: kai iš 10 mln. keleivių lėktuvu yra vienas teroristas. Jei detektorius ir patikrinimo procedūros 99.99% tikslumu nustato teroristus, tai bus pagautas vienas teroristas ir neteisingai apkaltinti 1000 paprastų keleivių.
Petras N., 2013-08-06 11:06:14
Antras:
Akivaizdu, kad antrąją seką sunkiau “pasiekti” nei pirmąją, nes ji tokia pati, tik su papildomu R pradžioje (1/3 mažiau tikėtina seka).
Trečioji nuo antrosios skiriasi tuom, kad vietoj 1/3 įvykio, turime 2/3 * 2/3 = 4/9 įvykį, kuris yra labiau tikėtinas.
Jeigu pirmosios sekos tikimybę prilyginsime 1,
tuomet antrosios sekos tikimybė lygi 2/3,
tuomet trečiosios sekos tikimybė lygi 8/9 (iš antrosios nuėmus 1/3 ir pridėjus 4/9 tikimybių įvykius).
Ats: Labiausiai tikėtina pirma seka, mažiausiai – antra.
Matas, 2013-08-06 11:28:06
O man dar patiko lengvas tikimybių uždavinukas: 0,8 tikimybė, kad turi savo namų raktą, o jei turi, tai 0,5, kad vienoje kišenėje, ir tiek pat kitoje. Pasitikrinini vieną kišenę – rakto nėra. Kokia tikimybė, kad jis kitoje kišenėje?
Rasa, 2013-08-06 11:37:28
Matui: Čia priklausomai nuo to, kaip labai tau reikia įeiti į tuos namus. Jei trepeni už durų ir labai nori į tualetą, tai manau beveik 99% tikimybė, kad rakto nebus ir kitoje kišenėje… 😀 Būsi jį pamiršęs draugės rankinuke… Su tokiais dalykais, kaip raktai, visad suveikia ne tikimybių teorija, o Merfio (t.y. kiaulysčių) dėsnis 🙂
Burgis, 2013-08-06 14:36:48
Matui: prašyčiau po savaitės pateikti savo uždavinio sprendimą. Atsilygindamas aš pateiksiu „Laukimo uždavinį“, kurį esu įtraukęs į konspektą studentams.
Burgis, 2013-08-06 14:38:33
Petrui N.: bravo ir… gaila, kad neleidote kitiems ilgiau pasikankinti.
Labai įdomus pirmojo uždavinio aiškinimas, bet ar visi supras?… Aš pateiksiu klasikinį matematinį sprendimą. Jau kaip aš mėgstu klasiką!
Smile, 2013-08-07 08:25:53
Rasai: papildysiu – Jūsų aprašytoj situacijoj dažnai būna, kad raktas būna pirmoj kišenėj, bet randi jį tik iš trečio karto – t.y. patikrinus pirmą ir antrą kišenę ir vėl grįžus į pirmą (ir tai ne iš karto). Ar matematikoje tokios tikimybės vertinamos ar čia jau “už skalės ribų”?
tulis, 2013-08-08 20:20:03
Na aš ne į matematinę šios knygos dalį atkreipsiu dėmesį. Įdomu ar knygoje yra paaiškinama visgi kodėl žmogeliukai atrodo vis didesni, o linijos nevienodo ilgio?
Iš tikrųjų net ne Jūsų psichologija trukdo tai suvokti, o paprasta, bet ne prasta, fiziologija.
Beje optinės iliuzijos labai įdomi tema. Gilintis, kaip smegenys interpretuoja ir lygina vaizdinius, kaip ir į kokią smegenų sritį sklinda impulsai, lemiantys iliuzijų sukūrimą bei kaip smegenys klysta lygindamos vaizdinius ir mėgindamos taip mažiau save apkrauti šiuo metu labai perspektyvi tyrimų sritis. Regos neurofiziologija tiriama ir mūsų LSMU klinikose ir galime šituo pasidžiaugti. 🙂
Artūras, 2013-08-10 16:48:18
Aš sakau, kad tai psichologija trukdo mums suvokti kai kuriuos dalykus. Tiesiog žmonės turi jau tam tikrą suvokimą apie mus supančią aplinką. Ir todėl jie tiesiog negali priimti kai kurių faktų. Mokslo pasaulyje to pavyzdys yra pirmoji atrasta egzoplaneta prie 51 Pegasi žvaigždės. Pagal stebėjimų duomenis buvo rasta labai masyvi (maždaug Jupiterio masės) ir labai trumpo apskriejimo periodo (4 dienos) planeta. Tačiau mokslininkai ilgą laiką nepatvirtino atradimo vien dėl to, kad atrodė neįmanoma, kad planeta turėtų tokį trumpą apskriejimo periodą apie savo žvaigždę. Nors jų naudojamas paieškos metodas savaime paprasčiau aptinka būtent masyvias trumpaperiodes planetas.
Burgis, 2013-08-13 16:00:19
Na, Matai, kaip išsprendžiate savo uždavinį? Savaitė praėjo…
*
Pateikiu D. Kahnemano uždavinio sprendimą. Tai klasikinis Bejeso teoremos pritaikymo uždavinys. Studentams sakau: jei apie tai, kas įvyksta tik su tam tikra tikimybe, pasakyta, kad įvyko – reikės Bejeso… Reikės patikslinti vienos iš hipotezių tikimybė: prieš įvykį hipotezės būna apriorinės, po įvykio -aposteriorinės. Na, užtenka gąsdinti žodžiais… :-).
*
Kokia tikimybė, kad liudininkas atpažino mėlyną automobilį? P(A)= 0,15*0,8+0,85*0,2 (automobilis buvo mėlynas ir liudininkas teisingai jį atpažino, arba automobilis buvo žalias, bet liudininkas klaidingai atpažino jį kaip mėlyną).
Pirmojo dėmens (pirmosios hipotezės dėmens) santykis su visa suma ir yra ieškomoji tikimybė 0,41.
*