Vienas svetainės lankytojas paprašė tokios temos, todėl rašau:
это я знаю и помню прекрасно пи многие знаки мне лишни напрасны…
pi=3,14159265358…
Taip, šiuo rusišku “eilėraštuku” irgi galima galima “sužinoti” skaičiaus pi skaitmenis (lietuvišką “eilėraštuką” rasite temoje “Pedagogų yra, trūksta Mokytojų”.
***
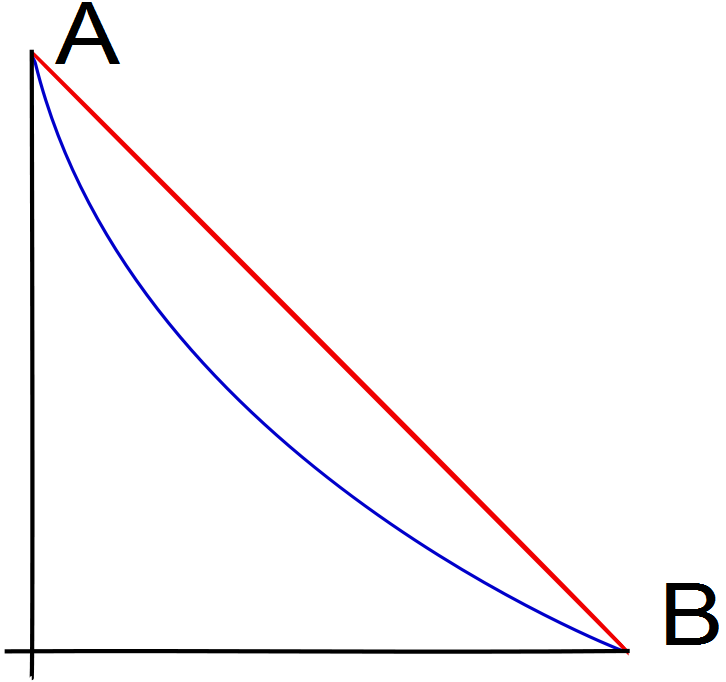
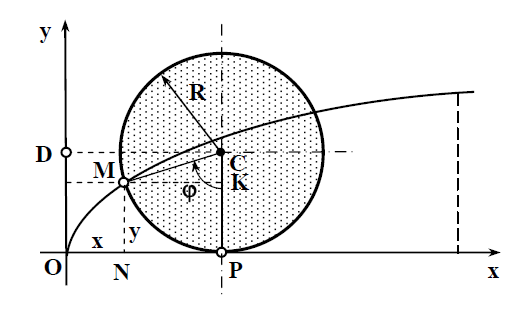
Kas yra įdomus uždavinys? Man įdomu stebėti (http://pl.wikipedia.org/wiki/Brachistochrona), kas yra brachistochrona, įdomu žinoti, kad tai cikloidės dalis, įdomu išspręsti, pavyzdžiui, tokį uždavinį: Apskaičiuokite cikloidės x = r(t − sint), y = r(1 − cost) (r > 0) pirmosios arkos ilgį. Pirmoji cikloidės arka gaunama, kai parametras t kinta nuo 0 iki 2π.
***
Kažkada vaikystėje mėgavausi J. Perelmano knyga “Įdomioji fizika”. Šiandien buvau šokiruotas radęs nemokamas abiejų dalių kopijas svetainėje www.fizika.lm.lt.
Jei susidomėsite, čia įdėsiu kai kuriuos SAT (populiaraus egzamino stojantiesiems į kitų šalių universitetus) matematikos uždavinius: jie mane žavi paprastumu ir originalumu.
***
Bet štai SAT anglų kalbos dalis man įdomi, bet per sunki:
adj. impartial
(a) commonplace
(b) incipient
(c) prevailing among animals
(d) unbiased
***
Todėl vaikams dažnai duodu spręsti tokį uždavinį:
Upės krante reikia pastatyti vandentiekio bokštą, iš kur vanduo būtų tiekiamas vamzdžiais į gyvenvietes A ir B.
Kurioje vietoje reikia jį pastatyti, kad bendras vamzdžių ilgis nuo bokšto iki abiejų gyvenviečių būtų mažiausias? (www.fizika.lm.lt).
***
Dar įdomesnis uždavinys apie keturis keliautojus, kuriuos pagavo žmogėdros (kažkur jis jau yra šioje svetainėje). Kažkas (gal aš?) pasakė, kad geri aktoriai geriausiai vaidina pauzes. Koks įdomus uždavinys, kai pauzė yra esminė informacija! Nepamenate? Pakartosiu.
IIII < < <
I___\__IIII____I ___I___I
Pagavo žmogėdros keturis keliautojus, užkasė į smėlį iki pat kaklo: tris vienoje sienos pusėje, ketvirtą kitoje. Visi – veidu į sieną. Uždėjo visiems kepures: dvi juodas, dvi raudonas. Ir sako žmogėdrų vadas: jei kuris nors iš jūsų pasakys, kokios spalvos jo kepurė, – visus paleisime, jei ne – mirsite. Ar išsigelbėjo keliautojai? Be abejo! Jei trečiasis kraštinis dešinėje prieš save matė dvi vienodas kepures, jis bematant pasakė, kokios spalvos jo kepurė. Bet jei jis padarė pauzę, tai savo kepurės spalvą pasakė vidurinysis iš trijų!
***
O dabar – jūsų eilė…
***
Papildyta: kadangi skaitytojai susidomėjo begalybės mistika, įdedu Kocho snaigę: baigtinis plotas, apribotas begaline linija!

Atsakymai
matematikos mokytoja, 2008-11-29 20:46:00
Labai gražus uždavinys: Sierpinskio nėrinių ploto skaičiavimas. Juodame trikampyje, kurio plotas 1, brėžiame visas vidurines linijas ir “išpjauname” vidinį trikampį. Tą patį pakartojame su gautais trimis naujais juodais trikampiais ir t.t… be galo daug kartų. Sudedame pradinio ir visų (be galo daug), po kiekvieno žingsnio gautų, juodų trikampių plotus ir gauname 4. Gražu, neįtikėtina. Panašus ir Sierpinskio kilimo ploto skaičiavimas.
Laurynas, 2008-11-29 21:36:43
Sierpinskio nėriniai: išpjautų trimapių plotų suma yra 1, ne 4. Tačiau modifikuotas pradinis trikampis turi įdomių savybių, pvz. jo plotas nulinis, tačiau perimetras (jei galima jį taip pavadiniti) yra begalinis.
matematikos mokytoja, 2008-11-29 22:07:41
Laurynui. Rašiau ne apie išpjautų, o likusių, juodųjų trikampių, plotų sumą kartu su pradiniu juoduoju. Kas liko išpjovus, ir yra Sierpinskio nėriniai. Visų nėrinių suma ir yra 4. 🙂
Burgis, 2008-11-29 23:20:44
Paaiškinkime Sierpinskio nėrinių mistiką taip: pradinio lygiakraščio trikampio plotas lygus 1. Vidurinėmis linijomis išpjauto vidinio trikampio plotas, akivaizdu, yra ketvirtadalis pradinio trikampio ploto (nes susidaro keturi lygūs trikampiai). Iš trijų kampuose esančių trikampių išpjauname po trikampį, kurio plotas yra ketvirtis ketvirčio = 1/16. Taigi antruoju “ėjimu” išpjauname 3/16 ploto. Trečiuoju ėjimu – 9/64. Po begalybės pjaustymų gauname S = 1/4+3/16+9/64+… = 1/4/(1-3/4) = 1. Taigi “išpjaustėme” visą trikampio plotą, nors po kiekvieno žingsnio kiekviename trikampyje “neišpjauto” likdavo tris kartus daugiau nei išpjauto!
O jūs kaip aiškinate?
matematikos mokytoja, 2008-11-30 00:16:49
Kas yra Sierpinskio nėrinys? Tai, kas liko išpjovus. Visų nėrinių suma (įskaitant ir pradinį – visą, jis irgi laikomas nėriniu): 1/(1-3/4) = 4. Mistika – sudedam be galo daug plotų, o gauname baigtinį skaičių 4. Beje, pradinis trikampis nebūtinai lygiakraštis.
Raimundas Zabarauskas, 2008-11-30 03:37:41
Pi atsimenu tik iki 10 ženklo:
Кто и шутя и прямо возжелает пи узнать число уже узнает
Galvosūkį prisiminiau seną bet gerą:
Burgis, 2008-11-30 09:28:27
matematikos mokytojai: gali būti, kad kas nors iš lankytojų (pavyzdžiui, aš…) Jūsų aiškinimų nesupranta, todėl pabandysiu savaip paaiškinti.
Dabar paklauskime, kiek ploto LIEKA po išpjaustymų (lieka nėrinys). Po pirmojo trikampio išpjovimo lieka 1- 1/4 = 3/4 ploto, po antrojo žingsnio (išpjaunami trys trikampiukai): 1- 1/4 – 3/16. Pratęsę procedūrą gauname, kad galutinis nėrinio plotas yra 0.
Tai, mano manymu, ir yra mistika, o ne tai, kad nykstamosios geometrinės progresijos narių suma duoda baigtinį skaičių. Visada taip yra. Žinoma, tai irgi mistika, bet Sierpinskio nėrinių atveju keliskart sumuoti tuos pačius plotus, įskaitant pradinį, – nesuprantamas noras…
matematikos mokytoja, 2008-11-30 11:23:45
-
Matematikų norai ir užduotys retai kam suprantami. Kaip Jūsų minėtame anekdote apie silkę, ką noriu tą ir sudedu, kad ir pasikartojančius plotus.
-
Užduotis ne mano sugalvota, paimta iš: P.Tannenbaumas, R. Arrnoldas. Kelionės į šiuolaikinę matematiką.
-
Šį uždavinį ir naudojau kaip iliustraciją to, kad nykstamos geometrinės progresijos narių suma yra baigtinis skaičius. Tai Jums visada taip yra, o mokiniams iki tokio suvokimo dar labai ilgas kelias. Vaikams įrodymas, kad “išpjovus viską” lieka plotas lygus 0, arba sudėjus “visus išpjautus” bus 1, nėra mistika. Bandžiau, šie pavyzdžiai jiems nepalieka įspūdžio. Jie teigia: kam ta progresija, jei ir taip aišku, kad taip turėjo būti.
matematikos mokytoja, 2008-11-30 12:10:06
Taip, Koch snaigė tikrai prasmingesnis pavyzdys, nes plotų sumavimas nėra dirbtinis, o reikalingas. Irgi mėginau, vaikams buvo labai įdomu. Rekomenduoju, kolegoms, ypatingai prieš Kalėdas.:)
i2243, 2008-11-30 16:53:21
Dėkingas autoriui uz teisingą temos atidarymą. Jei kam idomu bus pateiksiu keleta paprastų galvosukių, kuriuos galėtų spręsti betkokio amziaus smalsuolis. Manau , kad šis skyrius bus pagrindinis šios svetainės.
Man vienas protingas mokytojas pasakė daryk tai ką geriausiai moki. Todėl gerb. Br.Burgiui linkiu daryti ką darė iki šiol, o nebuti politiku.
i2243, 2008-11-30 17:39:03
-
Pi šioje int. nuorodoje: http://www.exploratorium.edu/pi/Pi10-6.html
-
neblogas uždavinys;
-
-;
4)http://www.fizika.lm.lt/index.php?option=com_content&task=view&id=465&Itemid=112
Kaip gaila , kad nelieka vietos pamastymui atsakymus nesunku rasti internete:(
Iš ties puikūs uždaviniai.
i2243, 2008-11-30 17:44:35
Uždavinys:
*******
Turima vaistinės pakabinamos svarstyklės ir 12 vienodos išvaizdos rutulių. Yra žinoma , kad 1-as iš jų yra skirtingo svorio. Reikia 3-im svėrimais nustatyti kuris iš jų.
************
Burgis, 2008-11-30 19:17:08
i2243: o taip, tai įdomus uždavinys vie todėl, kad nuo panašių skiriasi esminiu dalyku: nepasakyta, ar tas “kitoks” rutulys yra lengvesnis, ar sunkesnis. Sprendimą esu aprašęs savo “Niekam tikusioje matematikos mokymosi knygoje”, todėl leiskime skaitytojams, kurie nesutinka pasinaudoti internetu, pasikankinti… 🙂
Raimundas Zabarauskas, 2008-12-01 05:35:02
Šiek tiek ne visai į temą, bet štai įdomus algoritmas: http://www.rzu.lt/?2008-12-01.
Analitiškai šis uždavinys man pasirodė neišsprendžiamas (Xv = funkcija(Xa, Ya, Xb, Yb) ir Yv = funkcija(Xa, Ya, Xb, Yb)…).
Modeliuoti jį tikrai paprasta.
Ar edukologiškai prasminga?
i2243, 2008-12-01 09:46:49
Raimundau Zabarauskui: tai dar karta įrodoma , kad uždavinio sąlyga reikia skaityti atydžiai.
Iš 1-o karto uždavionį netaip supratau, tačiau pažiūrėjas atsakyma suvokiau suklydęs. 🙁
i2243, 2008-12-01 10:38:44
Prie to paties dar vienas uždavinys (dėl smulkių netikslumų atleiskite, nes cituoju iš atminties šaltinis yra žinomas).
Tėvas mirdamas paliko 3-im sūnams 17 kupranugarių. Liepė pasidalinti taip: jauniausiam 1/2 , viduriniam 1/3, o vyriausiam 1/9 viso turto.
Kaip padalinti sveikais kupranugariais?
i2243, 2008-12-01 14:44:16
Nepalikote galimybės nežinantiems pagalvoti. 🙁
Burgis, 2008-12-01 15:05:42
i2243: Pašalinau sprendimą, bet Jūs patikslinkite sąlygą…
i2243, 2008-12-01 15:39:49
DĖKOJU. Teks perversti archyvą. Pažadu kad ne tik patikslinsiu sąlyga, bet ir nurodysiu informacijos šaltinį.
grifas3000, 2008-12-01 21:15:29
Tikiuosi niekas neužpyks už tokį uždavinį:
Motina vyresnė už savo sūnų 21 metais. Po šešių metų ji bus už jį vyresnė penkis kartus.
Klausimas: kur tėvas?
Matematikų olimpiada 1969.
i2243, 2008-12-01 21:30:21
Arabas turėjo 17 kupranugarių ir 3 sūnus. Mirdamas jis jauniausiam sūnui paliko pusę, viduriniajam – trečdalį, o vyriausiajam – devintąją dalį savo turto. Pradėję dalybas broliai sutriko. Tada vienas jų pasiūlė pasiskolinti vieną kupranugarį iš kaimyno. Taigi jie turėjo 18 kupranugarių, iš kurių jauniausias brolis gavo 9, vidurinis -6 ir vyriausias – 2 kupranugarius. Vieną likusį kupranugarį jie grąžino kaimynui. Kaip paaiškinti šias dalybas?
Paimta iš:
1989 m. “Matematikos galvosūkiai” Aleksandras Baltrūnas
i2243, 2008-12-01 21:42:19
grifui3000: tai labai paprastas uždavinys. Salygos negali atitikti realaus atvejo, todel atsakymas: tėvo nėra. Tai isaiskeja sprendziant ligciu sistema.
GL, 2008-12-01 21:46:00
Gali, jeigu neigiamas amzius leistinas 🙂
Bet visgi net jeigu klausiama dienos tikslumu, manau kas atsakymas yra “95% tikimybe, kad negalima pasakyti” :]
i2243, 2008-12-01 22:40:26
taip skaiciuojant sprendimas butu. -3/4 metų tiek butu sunui tuo metu . Aisku kur butu tetis. Salia 🙂
i2243, 2008-12-02 09:30:48
Trys vairuotojai turėjo nuvežti 7 pilnas, 7 pripildytas iki pusės ir 7 tuščias statines. Kadangi visi turėjo vežti po vienodą krovinį, susiruošė tepalo įpilti į tuščias statines. Tačiau vienas vairuotojas pareiškė, kad tai nebūtina. Ir iš tikrųjų, tiek tepalą, tiek statines jis padalijo vairuotojams po lygiai, neperpildamas jų turinio. Kaip jis tai padarė?
Šaltinis tas pats.
1989 m. “Matematikos galvosūkiai” Aleksandras Baltrūnas
i2243, 2008-12-02 11:13:39
Siūlau skaitytojams neplėtoti knygų reklamos, bet pateikti savus originalius galvosūkius , uždavinius.
Truputi fizikos. Idealioje aplinkoje iš elektronų patrankos išaunama elektronai v greičiu. Kas darysis po to?
Raimundas Zabarauskas, 2008-12-03 05:20:40
Susimąsčiau: tema įdomi, bet tokia „monologiška“…
Antra vertus, kai kurių įdomiųjų uždavinių didaktinė funkcija siauroka (sukrėsti (apsimentant, kad taip skatinamas nestandartinis mąstymas)).
Būt įdomu pasikalbėti apie įvairių uždavinių edukologinę pusę (sakykime, dalykų integravimui ar kitkam).
i2243, 2008-12-03 08:52:16
Raimundui: nesuprantant šių galvosūkių , uždavinių aplamai čia niekas neįdomu ir kvaila.
Tikra istorija. Skrenda keliautojai oro balionu. Mato eina takeliu susimąstęs žmogelis. Kai oro balionas buvo netoli jo , oreiviai paklausė: “kur mes esame?”
Žmogelis pagalvojo ir atsakė: “Jūs skrendate oro balionu.”
Keliautojai vieningai nusprendė , kad tai buvo matematikas. Pagal ką jie taip nusprendė?
Raimundas Zabarauskas, 2008-12-03 08:55:03
Maždaug tą ir turėjau omeny.
Uždaviniai – slenksčio matuokliai?
Vainius, 2008-12-04 14:25:18
i2243, o koks atsakymas į tą su oro balionu?
Jis man truputį priminė klausimą, kuris kažkada buvo užduotas inverviu stojant į Oksfordą (berods, politiką su filosofija ir ekonomika): If you are not in California, how do you know it exists?
i2243, 2008-12-04 15:57:19
Vainiui: Tu teisingai atspėjai . Taip ir yra kaip sakai.
Antanas, 2008-12-04 16:05:17
Vainiau, atsakymas į klausimą apie oro balioną: todėl, kad žmogelio atsakymas buvo visiškai tikslus ir visiškai nenaudingas.
nesvarbu, 2008-12-04 16:34:54
Visa eilė pateiktų galvosūkių yra klasikiniai. Dauguma manau juos gerai žino. Laiptelis . Paskutinio klausimo atsakymai toks turi būti: 1. Jis pagalvojo;2 . Atsakymas absoliučiai tikslus; 3. Niekur jo nepanaudosi.
Vainius, 2008-12-04 19:32:12
Chm. Į jį turėtų būt ypatingai sunku atsakyt žmonėms, kurie dar tiki, kad matematika yra ir turi būti pritaikoma. 🙂
i2243, 2008-12-05 13:55:37
Na kaip pirmas laiptelis būtu baigtas, tačiau daugelis uždavinių liko neišspręstu. Kas išdrįs pratęsti diskusiją aukštesniame lygmenyje? ….
Raimundas Zabarauskas, 2008-12-05 23:47:54
Ar tokio pakanka?
Burgis, 2008-12-06 08:46:59
Raimundui: viau, kaip įdomu! Įdomu ir smaulkmenos, kaip padaryta…
Raimundas zabarauskas, 2008-12-06 20:29:12
Ačiū. Ar tiek paaiškinimo užteks (mokiniams?), ar reikia platesnio?
Burgis, 2008-12-06 20:54:26
Ačiū, Raimundai. Protingi supras, kvaili nepaklaus… Man tai – jau praeityje.
Raimundas Zabarauskas, 2008-12-07 05:30:45
Paskutiniojo sakinio nesuprantu (tačiau, matyt, nesu pakankamai kvailas, kad nebeklausčiau).
i2243, 2008-12-08 17:46:49
Pilstymo galvosūkiai. Yra 12 litru indas su pienu. Reikia nupilti 6ltr, kai turima 5 ir 8ltr tušti indai.
i2243, 2008-12-08 18:06:20
Nuostabus Gauso kūgių pavaizdavimas. Suprantamai paaiškintas ir jų atlikimas.
Raimundas Zabarauskas, 2008-12-08 19:40:16
Apie kiekvienos eilės Koch snaigę galima apibrėžti apskritimą, kurio centras sutaptų su snaigės centru, o plotas būtų toks pats, kaip ir snaigės.
Įdomu, kuri dalis snaigės perimetro atsidurtų tokio paskritimo viduje, o kuri – liktų išorėje?
Lygiakraščio trikampio atveju gavau 47% viduje (bet gal ir suklydau). O kokia tendencija (ir riba)?
matematikos mokytoja, 2008-12-08 21:49:33
Pagal apibrėžtinio apskritimo apibrėžimą visa “snaigė” turi būti jo viduje, o apskritimas ją tik liesti. Vadinasi “snaigės” plotas turi būti mažesnis už apskritimo plotą. Visas snaigės kraštas irgi turi būti apskritimo viduje. Jei dalis krašto išorėje, tai apskritimas jau neapibrėžtinis. Šiaip mintis labai įdomi, reiks patyrinėti. 🙂
Raimundas Zabarauskas, 2008-12-09 05:37:14
Kalbėjau ne apie apibrėžtinį apskritimą, bet apie lygiaplotį (su snaige).
http://www.rzu.lt/index.php?2008-12-09
matematikos mokytoja, 2008-12-09 15:37:57
Na va, nusišnekėjau: ne apskritimo, o skritulio plotas. Ir, atrodo, ne aš viena 🙂 Anglų ir rusų kalbose tos problemos nėra. Ir apskritimas ir skritulys apibrėžiami tuo pačiu žodžiu. Kodėl lietuviai prisikuria sau problemų?
Klausimai…, 2008-12-09 21:37:02
Circle – skritulys,
Circumference – apskritimas …
Raimundas Zabarauskas, 2008-12-10 07:40:01
O gal reikia imti ne lygiaplotį skritulį, bet begalinės eilės koch snaigės ploto? Intuicija man kužda, kad uždavinys išsprendžiamas…
matematikos mokytoja, 2008-12-10 17:19:03
Taip, tik “circumference ” tai uždara kreivė (funkcijos grafikas) arba skritulio (circle) – geometrinės figūros – kraštas, t.y. perimetras. O lietuviškasis apskritimas mokyklinėje matematikoje dar ir atskira geometrinė figūra. T.y. anglai ir rusai turi vieną geometrinę figūrą – skritulį, o lietuviai dvi: apskritimą ir skritulį. Vaikai painiojasi, kai kurie mokytojai, kaip pastebėjote, irgi :).
vvv, 2008-12-11 09:17:23
Mus mokė, kad apskritimas – tai ne geometrinė figūra, o uždara kreivė, kurios visi taškai vienodai nutolę nuo vieno taško vadinamo centru. O skritulys – geometrinė figūra, t.y. apskritimo apribota plokštumos dalis. Ar ši teorija jau pasenusi?
vvv, 2008-12-11 11:01:39
Beje, rusai irgi turi 2 sąvokas “круг” ir “окружность”, kur pirmoji reiškia skritulį, o antroji apskritimą.
Raimundas Zabarauskas, 2008-12-11 14:38:50
Nuo metematinės problemos nejučiom peršokome prie lingvistinės…
O vis dėlto, jei grįžtume? Snaigės keitimas lygiapločiu skrituliu nėra labai beprasmis veiksmas. Jį galima sulyginti su smulkių kranto linijos elementų aukojimu, brėžiant apytikrę liniją žemėlapyje.
Ar tokia linija turėtų būti vedama taip, kad plotas išliktų konstanta, ar kaip nors kitaip: sakykime, kad begalinio perimetro dalys, esančios abipus šios linijos, būtų lygios?
matematikos mokytoja, 2008-12-11 16:18:25
vvv: Kuriais metais? Kurioje klasėje mokė? Jei tarybiniais laikais, tai buvo: “…geometrinė vieta taškų, vienodai nutolusių nuo vieno taško…”. Dabar apibrėžimas toks: “Taškai, vienodai nutolę nuo vieno taško, sudaro figūrą vadinamą apskritimu”. Kreivės tikrai nebuvo ir nėra, nes ši sąvoka atsiranda tik vyresnėse klasėse kartu su funkcijos sąvoka, o apskritimas apibrėžiamas penktoje – šeštoje. Kur problema? Penktokui didelė. Trikampio kraštas nėra joks atskiras daiktas, o skritulio yra. Kodėl? (jie dar klausinėja 🙂
matematikos mokytoja, 2008-12-11 16:34:48
R.Zabarauskui. Dėkoju už idėją “Snaigės keitimas lygiapločiu skrituliu nėra labai beprasmis veiksmas. Jį galima sulyginti su smulkių kranto linijos elementų aukojimu, brėžiant apytikrę liniją žemėlapyje.” Nebūtinai kalbant apie Koch snaigę (jei atvirai, tai nelabai turiu kam tai papasakot), būtinai panaudosiu. Mano “ūkyje”, tai tikrai pravers.
Koks turėtų būti skritulys, galėtų priklausyti nuo situacijos: kas yra svarbesnis plotas ar perimetras? Jei plotas, tai lygiaplotis, jei perimetras, tai skritulys toks, kad kuo mažesnė jo dalis išorėje. Bet, turbūt aš neteisi…
smile@, 2008-12-14 19:54:11
Gal galetumete parasyti 6 klases uzdaviniu ar galvosukiu,nes visi cia labai sunkus.
Burgis, 2008-12-15 12:34:48
Ne, smile, kiekvienas sau mėgiamų dalykų turi surasti pats… Šiandien kursuose septintokams pateiksiu šį tą, kas gal ir tau ptiktų, bet aš juk nežinau, kas tau patinka…
super, 2009-10-14 19:56:26
Galvosukis, pabandyk isspresti,
mitinge dalyvauja x zmoniu, jeigu juos surikiuotume i eiles po 10, paskutineje eileje truktu 1 zmogaus; lygiai tas pats atsitiktu jeigu juos surikiuotumem i eiles po 9,8,7,6,5,4,3 ir 2. Kos zmoniu skaitcius dalyvauja mitinge (x mazesnis uz 5000) ?
Smagaus XD
Galvosukiai, 2011-11-23 12:49:14
Nu ir sunkios uzduotys…
Matas Bernunas 5a, 2013-05-30 21:17:31
kietai bet galletumeta ir geresniu uzdavinuku prideti ir ?NERUSISKU!