Jei aš nebesugalvočiau, ką rašyti šioje svetainėje, visada galėčiau pateikti savaitės įspūdžių suvestines. Man atrodo, kad kai kas galėtų jus sudominti…
*
Ši savaitė buvo itin įdomi. Vakarais kūrendavau židinį (lepinamės!), drybsodavau ant sofos ir žiūrėdavau, kaip TV rodo mūsų varganos politikos šalį… Kartais, žinokite, pasitaiko įdomių momentų! Pavyzdžiui, vakar vienoje laidoje susikirto Viktor Uspaskich, Arūnas Valinskas ir Algimantas Šindeikis. Mudviem buvo įdomu!
*
Kitoje laidoje buvęs mūsų šaunus gimnazistas Justas Jaruševičius pademonstravo debatų klasę! Aukšto skrydžio ISM studentas, aukšto!
*
Pasimėgavau seminaru Alytuje. Yra šviesių vietų! Dar apie tai parašysiu…
*
Mus aplankė 15 gimnazistų ir mokytoja iš Vilniaus Vytauto Didžiojo gimnazijos. Įdomūs ir mieli svečiai! Gavau dovanų jų išleistų knygų, gal kada apie jas parašysiu…
*
Dirbau matematikos mokytoju. Man patiko! Tik kojas pakerta…
Pateikiu jums vieną trečioko Prano uždavinį. Pranas pradėjo spręsti (iki sistemos), aš pabaigiau, bet įtariu, kad galima trumpiau. Neturiu įgūdžių… Bet man vis dar įdomu!
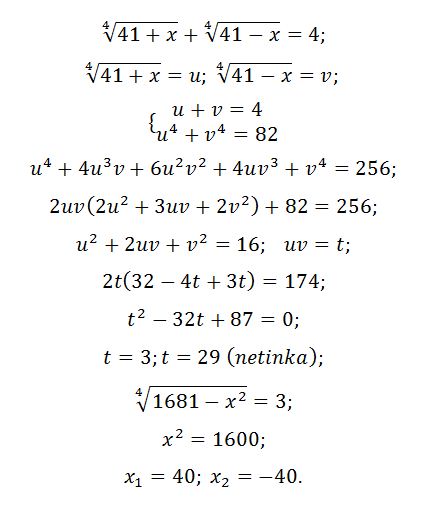
Kaip jūs spręstumėte?
Atsakymai
Burgis, 2012-11-23 12:04:11
Įvertinkite…
petras, 2012-11-23 13:17:10
Tokio sprendimo pats nesugalvočiau tikriausiai (nes man atrodo, lyg pateiktas pvz. gali būt vienintelis ir tai pasirodė sudėtingas), todėl mėginčiau spėjimo būdu 🙂 pasisekė, kad skaičiai maži, tai mum tinka: 0+4;1+3;2+2;3+1;4+0, ir greitai randu atsakymą (pasisekė). na o jei atsakymo nebūtų, tai su nesveikais skaičiais tikrai neprasidėčiau, juk bendrą kalbą su tokiais sunku rast.
ir šiaip truputi ne į temą. kažkaip per matematiką būdavo, kad pvz. vietoj įprastinių kintamųjų žymėjimo panaudoja mokytojas ar dėstytojas kitas raides ir ne vienas moksleivis/studentas suglumsta, tipo, mes to nesimokėm :DD tai smagu, kad va paįvairina studentai kartais kintamuosius vietoj įprastinių a,b,c, į u v t. ir pan. net padvelkė truputi fizika 🙂
miklis, 2012-11-24 01:22:28
Iki sistemos sprendimas toks pats. Vėliau – tradiciniai keitiniai u+v=a ir uv=b Toliau labiau pratusiems man rodos turėtų būti nesunku atlikt pertvarkymą u^4+v^4=(u^2+v^2)^2-2u^2v^2=(a^2-2b)^2-2b^2={žinant, kad a=4} 256-64b+2b^4=82, čia b skaičius, lygus t pavyzdyje. Toliau spręsčiau labai panašiai.
Sunkiausia dalis yra matyt tesingas a ir b radimas. Tai – labai savotiškos matematikos atšakos dalis. To net nežinodami, mes rėmėmės pagrindine simetrinių polinomų teorema, kuri teigia, kad bet koks simetrinis kelių kintamųjų daugianaris yra visada išreiškiamas per elementariuosius daugianarius. Šiuo atveju f(u,v)=u^4+v^4 yra simetrinis, nes f(u,v)=f(v,u), o elementarieji yra u+v, uv. Elementarieji – tai visi tokie daugianariai, kurie tenkina simetriškumą, o kiekvieno kintamojo laipsnis juose lygus 1. Mokykloje sprendžiami uždaviniai su dviejų kintamųjų simetriniais daugianariai. Tačiau manau mokymo programoj stipresniems mokiniams galima pateikti uždavinių su trim kintamaisiais. Pvz.: išreikšti a^3+b^3+c^3 per a+b+c, ab+bc+ca, abc. Na, pakaks teorijos :). Norėjau tik pasakyt, matematikos taisyklė yra visur ieškoti bendresnių atvejų, o šie pavyzdžiai gal ką įkvėps.
Burgis, 2012-11-24 09:24:16
Tai bent miklis! KTUG turi kuo džiaugtis.