
*
Kokios mažos ir drovios buvo šios našlaitės visai neseniai… O dabar štai užaugo, išstypo ir… beveik nuleipo. Tai reiškia, kad valstybiniai brandos egzaminai netoli! Ką pagavęs už skverno bandau pamokyti, patarti. Skubu. Ir Sokolovas ragina…
*
Na, susikaupkite, paspręskite!
*
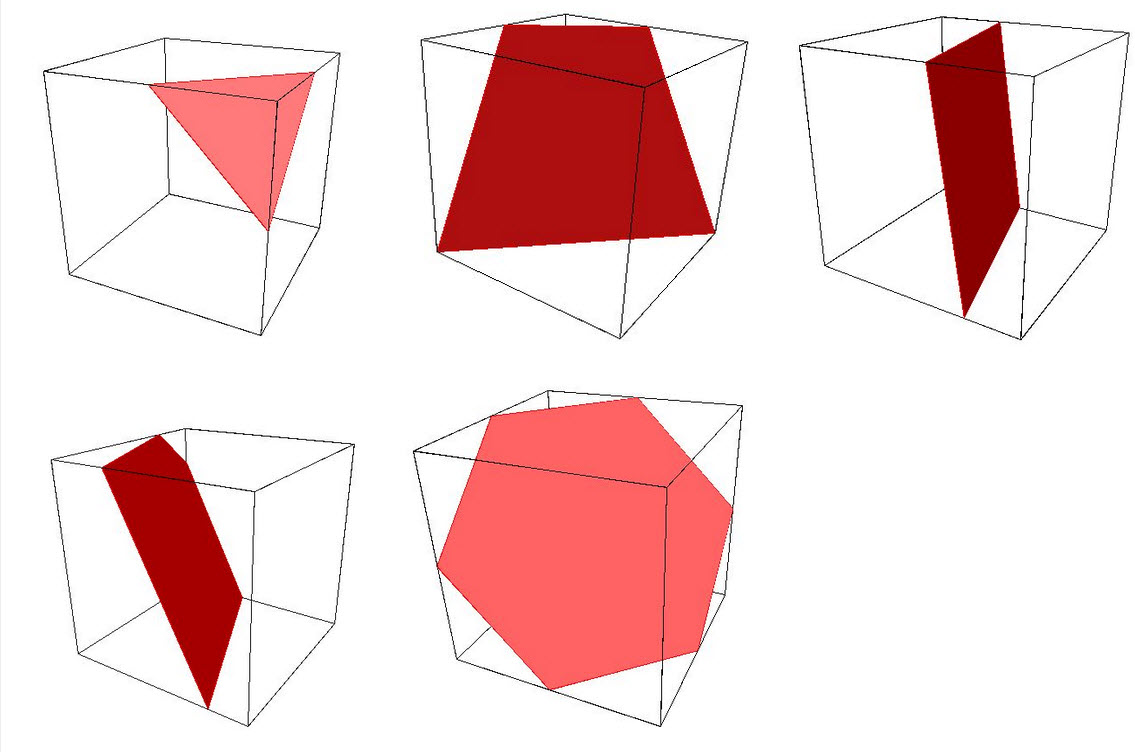
- Į rutulį įbrėžtas kubas, kurio medžiaga yra kitokios spalvos nei likusi rutulio dalis. Rutulys perpjaunamas per centrą į dvi dalis.
Kokį vaizdą matome pjūvyje? Ką GALIMA PAMATYTI pjūvyje?
*
Atlikite eksperimentą su skirtingų klasių moksleiviais – visiems vienu metu duokite šį uždavinį. Pamatysite įdomų rezultatą…
***
- Maišelyje yra penki rutuliukai: trys juodi ir du balti. Atsitiktinai ištraukiami trys rutuliukai. Kokia tikimybė, kad du iš jų juodi?
*
Pirmas sprendimo būdas. Visos galimos eksperimento baigtys yra tokios: JJJ,JJB,JBJ,BJJ,JBB, BJB,BBJ. Iš šių septynių baigčių trys yra tokios, kai ištraukiami du juodi rutuliai. Vadinasi, ieškomoji tikimybė yra 3/7.
Antras sprendimo būdas. Klasika…
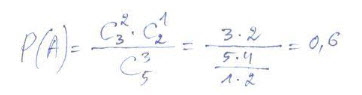
Kodėl skirtingi rezultatai?
***
Dėmesio! Prašau Sokolovo – neparašykite net užuominos!
*
O kiti juk nespręs, tiesa?
Atsakymai
Rasa, 2017-05-17 00:34:55
Mes (kas nors 🙂 sprendžiam, bet nesisprendžia 😛 T.y. aš tai galvoju tik, spręst nemoku. Tai ko gero mane prie pirmokų priskirt reikėtų 🙂
Tai gal pirmam matytume arba kvadratą arba stačiakampį, t.y. įvairių dydžių stačiakampius galima pamatyt manau, priklausomai nuo to, kaip pasuktas gausis tas kubas rutulio viduryje, kai pjausim 🙂 O ką svarbaus ten galima pamatyt didžiosiom raidėm, tai jau mokantys matematiką turi atsakyt 😛
O antram tai gal pirmas variantas kad tokia tikimybė, kai dar stovim prieš kamuoliukus, kai dar netraukėm, gal būt ji kinta po pirmo ištraukto kamuoliuko ir paskui vėl po antro? Gal antram sprendimo būde įvertinta pilna tikimybė? 🙂
Nu nežinau nežinau…
Einu geriau miegot, turbūt nusišnekėjau labai 😛
Sokolovas, 2017-05-17 06:27:57
DUOKITE MAN DAR TRUPUTĮ LAIKO, IR AŠ BAIGSIU TAI, KO NESPĖJAU PRADĖT
Alfa ir Omega…
Pirmoji ir Paskutinioji…
Rasai:
Puiku! Puiku, kad domitės! Gilinkitės dar, ir pajausite nuostabų kontaktą su šiuo Paslaptinguoju Pasauliu…
Mokančių matematiką žmonių nėra. Nes mes, šio pasaulio gyventojai, negalime pažinti už mus galingesnės erdvės. Mes galim tik siekti, galiausiai- tik TRUPUTĮ GAUDYTIS šioje Paslapčių Karalystėje…
Ne, nėra mistikos. Bet yra nepažintų reiškinių…
Ši nuostabioji Karalystė sveikina kiekvieną atėjusį, ir neliūdi išeinančių. O išeinantys, kad ir kiek jie siektų bei skverbtųsi, lemtingu valandą ištars- duokite man dar nors vieną akimirką, ir aš pabaigsiu tai, ko nespėjau pradėt…
Gilindamiesi į tikimybių teorijos paslaptis, iš pradžių išspręskime tokį uždavinį:
Du kartus metame simetrišką monetą. Kokia tikimybė, kad abu kartus atvirs herbas?
Tai- pradžia. Pradžia kelio, nepripažįstančio pabaigos.
Tai- Pirmoji pažintis. Ir ji atmeta pragmatizmą! Antraip ji būtų ne pirmoji, o paskutinioji…
Rasa, 2017-05-17 12:30:27
Nu, žodžiu… Ponas Burgis gudrauja 😛
Antram uždavinyje. Pirmas variantas, turi būti 4/7, kadangi keturios baigtys, kai du juodi rutuliukai ištraukiami, nes jei tris juodus ištraukiam, tai vis vien skaitosi. Tai bus JJJ, JJB, JBJ ir BJJ. Taigi 4/7. Jei imam ir padalinam, gaunam 0,57, taigi suapvalinus 0,6 🙂 Taigi abu variantai teisingi, tik aš antro nesuprantu 🙂
Giedrius, 2017-05-17 12:41:57
1-am uždavinį turėtume pamatyti kvadratą, stačiakampį, rombą (lyg tai ?) ir šešiakampį apskritime.
Rūta, 2017-05-17 12:42:59
Spręsim. Klasiką jau pamiršau (gėda), bet ant pirštų skaičiuoti dar moku. Todėl pabandysiu 🙂
Uždavinio apie rutuliukus pirmas sprendimas turbūt duotų tokį patį atsakymą, jeigu juodų rutuliukų būtų ne tik 3, o 13, 33, 333 ir dar daugiau (juk baigčių sąrašas atrodytų taip pat), bet juk suprantame, kad tikimybė būtų ne tokia pati. Nesvarbu, kokia eile krenta, svarbu, kad juodų yra daugiau nei baltų, o tai pirmam variante mano galva niekaip neįvertinta. Taigi, kamuoliukus numeruoju. Mano galimas baigčių sąrašas JJJ, B1J1J2, B1j2J3, B1j1J3, B2J1J2, B2j2J3, B2j1J3, BBJ1, BBJ2, BBJ3. Bet kodėl aš gaunu 7/10 :))))? Į kelintą man klasę? :)))?
Sokolovas, 2017-05-17 12:54:39
Rūtai:
Jūs gavote tikimybę, jog juodų rutuliukų bus du arba trys. O reikėjo tikimybės, kad bus DU juodi rutuliukai.
Akivaizdu, jog šiam įvykiui palankios yra šešios, o ne septynios baigtys…
Rūta, 2017-05-17 13:00:20
Ak, štai kaip!!! Ačiū už pagalbą, paprotinimą ir už smagią smegenų mankštą :).
Rasa, 2017-05-17 13:07:39
Giedriui: na man pirmam uždavinyje trūksta aiškumo 🙂 Aš mintyse jį nusilpdžiau iš plastelino, ir turbūt padariau klaidą, nes padariau abu pilnavidurius 🙂 O sąlygoje kubas tik įrėžtas. Kaip jį ten įrėši? Nebent su tokiom staklėm, kaip mano vaikas dirbo… Hmmm. O tada rutulys “tirštas”?, nes jei pav. į raudoną rutulį tik įbrėši kubą ir perpjausi, gali matyt ir tik dvi lygiagrečias atkarpas, jei kubas nepilnaviduris. Nu man tai reik žinot ar jie pilnaviduriai spalvoti ar tušti. Nes tada kitaip ir persimatys.
Rasa, 2017-05-17 13:15:30
Ir dar Giedriui: bet rombą vis vien kažkaip sunku išpešt, man tai jo nesimato 🙂
v., 2017-05-17 14:05:46
-
Galima pamatyti keturkampį (kvadratą, stačiakampį, rombą) arba (atrodo) šešiakampį.
-
Nes pirmas sprendimas neteisingas. Reikėtų įsivaizduoti kad kamuoliukai turi ant jų užrašytus numeriukus: J1, J2, J3, B1, B2, bet jų išdėstymo tvarka nesvarbi. Tada kombinacijos bus tokios: J1J2B1, J1J2B2, J1J3B1… Iš viso 10 kombinacijų, iš kurių palankios 6.
Vilkas Pilkas, 2017-05-17 14:56:21
Rasai:
yra žinoma, kad rutulio ašinis pjūvis yra skritulys (pilnaviduris). Kaip manote, ar Leonardo da Vinčio į kvadratą ir apskritimą įrėžtas Vitruvijaus žmogus yra “tirštas” ar “tuščias”?
…o dabar įsivaizduokite, ką pamatys žmogus su pjūklu perpjovęs sferą pusiau bet kaip, nes sferos paviršiuje nesuras įbrėžtinio kubo viršūnių… o dar jei jo žvilgsnio į pjūvį perspektyva nėra statmena pjūviui… plastilino Jums neužteks
Rasa, 2017-05-17 15:28:33
Vilkui Pilkui: Mhm. Kam žinoma, o kam ir pamiršta 🙂 Nes man ir eglutės žaisliukas rutuliukas 🙂 O ką gausi perpjovęs? Na bet kokiu atveju apvadas bus skritulys 😛
Vitruvijaus žmogus. Jis tuščias. Jis nupieštas plokštumoj. Jo nepasuksi. Arba aš tavęs nesuprantu 🙂
O jei į pilnavidurį rutulį idėsi, t.y. įrėši kubą. Nu tai sakau, kad tada kitaip matysis. Visaip. Gali net tik taškai keturi matytis. Tos spalvos kaip kubo linija. Mėlynos 🙂 Nes rytulys gražu raudonas.
Giedrius, 2017-05-17 16:13:48
Rasai: užduotyje pasakyta, kad įrėžtas kubas, kurio medžiaga yra kitos spalvos. Reiškia kubas yra ne tuščiaviduris (o gal tuščiaviduris, tik išorinės sienos iš kitos spalvos?). Bet veikiau, kad netuščiaviduris ir yra užpildytas kitos spalvos medžiaga. Taigi, perpjovę rutulį, matome pjūvį, t.y. plokštumą. Ir ką gi mes ten matome? Matome skritulį kažkokios tai spalvos į kurį yra įrėžta kitokios spalvos medžiaga. Jeigu kubas tuščiaviduris, tai skritulyje pakankamai aiškiai matytume tam tikros formos skylę, bet vis dėl to sąlygoje pasakyta, kad yra kitokios spalvos medžiaga. Tai ją mes ir turėtume matyti kaip ne kaip.
O dėl rombo. Jeigu pjauname kubą (kartu su rutuliu žinoma) tiesiog statmenai per centrą ir pjūvio plokštuma yra lygiagreti dviems kubo sienoms, tai pjūvyje matysime kvadratą. Bet jeigu tą kvadratą pastatome ant vieno kampo (o kubą ant vienos briaunos), tai jau turime rombo giminaitį 🙂 kvadratą, stovintį ant viršūnės. Ir jeigu dar pjūvio plokštuma eina ne lygiagrečiai dviems kubo sienoms, o šiek tiek kampu, tai šitas kvadratas turėtų išsitempti į viršų ir pavirsti rombu.
Lyg ir taip mano įsivaizduojamas plastilininis modelis galvoje rodo :)))
Vilkas Pilkas, 2017-05-17 16:22:53
Rasai: vienas Tamstos teiginys nepaneigiamas “rutulys gražu raudonas”. Kazimirui Malevičiui gražu juodas kvadratas… keturi taškai? Na gal polinėje koordinačių sistemoje… atleiskite už sarkazmą, bet letenos nusviro…
Vilkas Pilkas, 2017-05-17 16:31:09
Giedriau, jei jau pradėjot, neapribokit Rasos vaizduotės (keturiais) kampais…
Rasa, 2017-05-17 16:41:45
Vilkui Pilkui: Na aš į tavo pilnavidurį rutulį įdėjau kubo rėmelį. Nes taip supratau iš naujo “įrėžtas”. Sienų nepadariau, kiauras palikau. Ir gavosi taškai. Kai perpjoviau. Viskas čia logiška. Ką aš kalta, kad tau fantazijos trūksta kaip Malevičiui… 🙂 Ir aukštyn nosį, jei letenos nusviro 🙂 Nieko sau, matai nesupratau iš kažkelinto karto. Edisoną prisimink! Užtat kiek dabar visko žinau kas netinka! 😀
Giedriui: tai dėl rutulio išsiaiškinom, jis pilnaviduris. Vilkas Pilkas sako, turbūt žino. O su tuo kubu neaišku ar jis būna tik iš sienelių ar irgi turi būt pilnaviduris visas.
Nes pav. aš dar galiu įsivaizduot ir tuščiam rutuliuky (vat kaip eglutės žaisliuke) įdėtą iš vielytės kubą. Tada visos linijos visų matosi kai perpjauni. Bet tada tuščios linijos ten, ne plokštumos juk. Tai vėl kitaip.
Nu žodžiu aš tai važiuoju pas draugę arbatos gert 🙂
Giedrius, 2017-05-17 16:44:32
Vilkui Pilkui: Na, čia tik vienas iš variantų, o toliau jau… jungiam vaizduotę… ir kas žino kur jį nuneš… 🙂
Burgis, 2017-05-17 18:06:58
Nieko sau! Tik aš išvažiavau – jie puolė spręsti uždavinius! Žaviuosi! Ir stebiuosi, kaip tie mokytojai sugeba pateikti sąlygas, kad moksleiviai jas suprastų vienodai… Ne, jūs negalite! „Įbrėžtas“ tapo „įrėžtu“, kubas, pasirodo, yra tuščiaviduris…
*
Pirma – apie antrąjį uždavinį. Prizas „v.“ Taip, studentai ir moksleiviai užmiršta „sunumeruoti“ objektus, todėl tokios klaidos, kaip aš parodžiau, labai „madingos“.
*
Antrąjį uždavinį aiškinu suprantamai.
Užmiršk tą rutulį. Aišku, kad bet kuris jo pjūvis per centrą yra skritulys, apribotas apskritimu (o gal skritulys gali būti kitoks?…).
Galvok tik apie kubą. Iš bulvių ar arbūzų prisigamink kubiukų ir pjaustyk juos įvairiai – taip, kad pjūvis būtinai eitų per kubiuko centrą. Ką matai pjūvyje? Ar tai kartais yra toks kvadratas, kurio viršūnės liestų rutulio pjūvio apskritimą? Ne, nėra tokio kvadrato! O kaip tik tokį pjūvį jums nubraižys bent penki iš dešimties mokinių. Patikrinkite…
O kokie kiti galimi pjūviai?
Sokolovas, 2017-05-17 21:09:49
Gal jau galiu ir aš pakomentuoti antrą uždavinį…
Manau, jog pirmoji teisingą kelią įžvelgė Rūta. Ji sunumeravo rutulius…
“Pirmasis sprendimo būdas” yra įžymiosios Dalambero klaidos išraiška.
Antrasis sprendimo būdas-“klasika”,- suprantamas mokantiems kombinatoriką.
Yra dar vienas, gan abiturientų mėgstamas, sprendimo būdas:
P(A) = (3/5)(2/4)(2/3)*3 = 0,6.
Dėkui, gerb. Burgi ! Jūs tikrai sudominote žmones…
Rasa, 2017-05-17 21:20:12
Ir viskuo kalčiausias tas Vilkas Pilkas 🙂 Menininkas tikras. Tai jam Malevičius, tai da Vinčis. Ir sakė plastelino neužteks, kai norėjau susipjaustyt kubiuką kaip Burgis arbūziukus… O dabar vėl iš naujo viską galvot… 🙂
Taigi apibendrinam visų nuomones: raudonam apskritime gali būti mėlynas kvadratas (kaip noriu taip spalvinu :), stačiakampis, šešiakampis ir rombas 🙂 Jie žinoma gali kisti pagal pjovimo kampą.
Kas rado daugiau?
Rasa, 2017-05-17 22:01:04
Nu bet jei sąžiningai tai jei mintyse įlipinu kubą viduryje, tai ir pjaunant per kubo centrą pjaunasi ir pjūvyje vargu ar bus šešiakampis, turbūt nebus 😛
Rasa, 2017-05-17 22:25:23
Nu viskas. Daugiau nekomentuosiu 😛 Viską žinau. Šešiakampiai bus irgi. Nes jau galiausiai kad ramiai miegočiau vizualizavom su SolidWorks-u 😀 tą raudoną su mėlynu ir viską apžiūrėjau. Visaip iškraipėm 🙂
Buvo labai gražu 🙂
Burgis, 2017-05-18 10:02:04
Ačiū Rasai už atkaklumą!
Įkėliau paveikslėlį… Visko yra žiniatinklyje! Tik jūs patys įsitikinkite, kad svarbiausia klaida – nėra tokio pjūvio, kuriame kvadratas visomis viršūnėmis liestų apskritimą. Tokia buvo šios užduoties esmė….
Rasa, 2017-05-18 10:19:27
Atsiprasau kad rasau sveplai bet as masinoj 🙂 Taip, google visagalis 🙂 Bet va noris atsakymus islipdyt is to plastelino kur galvoj 🙂 Buvo labai smagu 🙂 Ir kokie kiti geranoriski, kaip stenges padet! Tik Vilkas Pilkas kantrybes mazai turi, turbut jis dar neturi vaiku 🙂 Paskui jau ismoksti but kantrus 🙂 Bet jis gerai moka viska labai. Ir Giedrius saunuolis! Aciu visiems. Ir zinoma sunui kuris vakare man viska nubraize pagal mano pageidavimus 🙂 Nerealiai idomu tas SolidWorkas.
Vilkas Pilkas, 2017-05-18 12:26:01
Rasai: lenkiu žemai prieš tamstą galvą, už tai kad modeliavot situaciją su SolidWorks (būt užtekę ir Sketchup’o).
Neapsigaukite su autoriaus pateiktu paveiklsiuku – ne visi variantai atitinka sąlygą. Be to, klausimas “ką galima pamatyti” matematiškai slidus, juk iš “šoninės” pjūvio plokštumos perspektyvos (projekcijos) pats pjūvis bus linija… Deja, gerb. Rasa, ne taškai, nes matematikoje negalima painioti apskritimo su skrituliu. Matematikui Jūsų eglutės žaisliukas bus ne rutulys, o dvi sferos tarp kurių yra stiklas…
O dabar parašykite, kad su Solidworks jums perpjautų per pusę hiperkubą.
Sokolovas, 2017-05-18 13:47:40
ARTĖJANT VASARAI
Kol neataušo…
- Yra šešios kortelės su raidėmis, iš kurių sudėtas žodis VASARA.
a) Užsimerkę imame keturias korteles po vieną, atgal negrąžindami. Kokia tikimybė, kad iš paimtų keturių kortelių galima sudėt žodį RASA ?
b) Užsimerkę imame keturias korteles po vieną , ir dedame jas eilės tvarka. Kokia tikimybė, jog susidarys žodis RASA?
- Vidutiniškai 20 procentų šalies merginų neateina į sutartą pasimatymą. Vaikinams šis rodiklis mažesnis- persigalvoja, ir į sutartą pasimatymą neatvyksta vidutiniškai 10 procentų šalies vaikinų.
Kiek procentų iš anksto sutartų pasimatymų neįvyksta?
petras, 2017-05-18 14:57:22
visi įvykiai 50/50, tikimybė 0,5. susidės žodis arba ne, atvyks į pasimatymą arba ne 🙂
Sokolovas, 2017-05-18 15:06:40
Petrui:
Tikimybė yra objektyvi, ji nepriklauso nuo mūsų norų.
O nevienodai tikėtinų baigčių skaičių santykis veda prie Dalambero klaidos…
petras, 2017-05-18 15:21:26
Gal ir objektyvi, bet ne reali 😉
Giedrius, 2017-05-18 15:46:17
Sokolovui: 1-as uždavinys. Šaunu beveik aklai, nežiūrėdamas į knygą ir nesikartojęs formulių :), bei paskaičiavęs paprastuoju būdu (ant pirštų). Juk kartais ir aklai vištai grūdas pasitaiko :)) Ats.: 1/60
Rasa, 2017-05-18 18:37:36
Sokolovui: ar bent truputį gali būt panašu į tai, kad 1. a) apie 0,27? 🙂
Vilkui Pilkui: SolidWorks, o ne kita, nes su ta programa sūnus dirba 🙂
Dėl Burgio paveiksliuko ir sąlygos, tai irgi ginčytina 🙂 Juk jis nurodė, kad bus pjaunama per vidurį skritulys, bet nenurodė kur bus įlipintas, t.y. įbrėžtas tas kubas. Mes, t.y. aš, įsivaizdavau, kad tai kubas, didelis koks tik telpa, bet realiai jis galėjo būt mažiukas ir šone, tada paveiksliuky visi nurodyti kubo pjūviai teisingi 🙂 Ar ne? Nes jei kubas didelis, tai pjaudami per rutulio centrą, pjausim ir per kubo centrą, o jei kubiukas mažiukas, bus kiti vaizdai 🙂 Tik, žinoma, manau, kad ne visi įmanomi šiuo atveju, t.y. su vienu kubu vienam rutuliuke. Raudonam 🙂 Bet juk jis tiesiog parodė, kas įmanoma išgaut iš kubo 🙂
O dėl hiperkubo, tai aš jau apžiūrėjus jį seniau, kiek mano protas pajėgus priimt 🙂 Tai tas pats daiktas, kur gali gautis visokiausios mandalos, jei žiūrime dvimatę projekciją ant lapo, o jei išvyniojam į trimatę, gaunas Salvadoro Dali nukryžiuotasis (nes tu čia matematiškas menininkas :), o kai jis neišvyniotas, kai keturmatis, tai man sunku suvokt, bet labai gražu vis vien 🙂
Sokolovas, 2017-05-18 20:14:34
Rasai:
1a) Ats: 1/5 (arba 0,2), b) Ats: 1/60.
Rasa, 2017-05-18 20:31:23
Burgiui: grįšiu jau greit 🙂 Po kokių 5 metų, kai mažoji ims eit 🙂 Na tai mokykloj darai kaip nori mokytojas (bent taip buvau dresuota :), o čia tai ir įdomu, kad gali pasvarstyt 🙂 Aš juk dėl to, kad kai Jūs įdėjot tuos paveiksliukus ir pav. trikampukas kaip pirmam tai juk nesigautų pagal Jūsų sąlygą jei kaip visi suprastum?
Mokykla… 😀 Visi mokosi skaičiuoti. Pirma klasė. O aš moku. Mokytoja liepia visiems namie pasidaryti tokius ryšulėlius iš degtukų su nupjautom galvytėm. Surištus po dešimt. Dešimt ryšulėlių po dešimt, nes mokysimės dešimtas dalis, dešimtis tiksliau. O aš nepadariau, nes man labai viskas ir taip buvo aišku. Visiškai aišku. Tada gavau pirmą gyvenime nuobaudą- tašką. Nes reikia ir viskas. Reikia viską daryti kaip visi. Turėjau visus visus penketukus ir vieną TAŠKĄ! Dabar nepamenu kur jį įlipdė- ar iš drausmės ar iš tvarkos… Pasidariau tuos pagaliukus, atnešiau, pasidėjau. Mokytoja sako: tai gali jų nenaudot jei mintinai skaičiuot moki… 🙂
Bet jūs man kas nors geriau paaiškinkit kas ta ketvirta dimensija kur hiperkubas gyvena? Lietuviškai sunku suprast tai dar įdomų anglišką filmuką radau, tada dar sūnų įkinkiau kad verstų ką sako, nors ir pati kaip ir supratau, nes ten juk pasakoja pridėdami po vieną. O penkta? O šešta?
Sokolovas, 2017-05-18 21:12:36
Rasai:
Jums lengviau bus suprast nuo dalies (b)
Tikimybė, kad pirma paimta raidė bus R, lygi 1/6.
Kad kita bus A, -3/5. Trečia raidė bus S su tikimybe 1/4, ketvirta A (iš likusių dviejų tokių raidžių) bus su tikimybe 2/3. Sudauginę šias tikimybes, gausime 1/60.
Dabar einam į (a) dalį.
Kiek keturraidžių žodžių (nebūtinai prasmingų) galima sudaryt iš Jūsų vardo raidžių? Manau, jog šis klausimas Jums turėtų būt įdomus.
RASA, SAAR, SARA, RSAA…Tai kiek?
Iš pradžių sudauginame 4*3*2*1=24. Tačiau yra dvi vienodos A raidės, todėl visų keturraidžių žodžių skaičius yra 24/2 =12.
Dalyje (a) reikia rasti tikimybę, jog traukiant keturias korteles, bus ištrauktos Jūsų vardo raidės bet kokia tvarka, t.y nesutvarkytas rinkinys {R,A,S,A} Todėl tikimybė bus 12 kartų didesnė už sutvarkyto raidžių rinkinio (R,A,S,A)pasirodymo tikimybę. Taip ir gauname 12*(1/60) = 1/5.
Sokolovas, 2017-05-18 21:24:22
Dar Rasai:
Nereikės grįžt į mokyklą, jei nuolat taip domėsitės, konsultuositės, mėginsite spręsti. 🙂
Galite dar apskaičiuoti:
a) Kiek skirtingų devynraidžių žodžių (nebūtinai prasmingų) galima sudaryt iš devynių žodžio
SOKOLOVAS raidžių?
b) Kokia tikimybė, kad atsitiktinai paėmus penkias šio žodžio raides, ir jas sudėjus traukimo tvarka (į dešinę), gausime žodį VOKAS? 🙂
Burgis, 2017-05-18 21:31:14
Sokolovui ir Rasai: (a) sprendimą aš linkęs pateikti klasikiniu variantu: (C(1;1)*C(1;1)*C(3;2))/C(6;4)…
*
Bet pradedantiesiems rekomenduoju sunumeruoti VASARA raides ir surašyti visus rinkinius po 4 raides – tai juk tik 15 rinkinių.
Rasa, 2017-05-18 22:54:00
Kosmosą gavau :/
Sokolovą galima sudėstyti į 60480 žodžių, o kad iš jo padarysim voką, tikimybė 1/2520
:/
Rasa, 2017-05-18 22:57:27
Net prisiminiau savo mylimą matematikos dėstytoją. Litvaitienė buvo. Jai būtų gėda už mane. Ir ji pasakytų man tai, ką kitiems sakydavo, man tai niekada nėra sakiusi 🙂 Ji tokiu ramiu rimtu veidu, tokia ilga ir kūda kaip šakaliukas, išdidžiai mosteldavo ištiesta ranka pirštais žemyn: “sėsk, zuikuti, du…”
Sokolovas, 2017-05-19 06:21:46
Rasai:
Žodžių dvigubai mažiau, nes tris vienodas O raides galima išdėstyti ne trimis (kaip Jums atrodė), o ŠEŠIAIS būdais: 3*2*1 =6
Jei visos 9 raidės būtų skirtingos, tai devynraidžių žodžių būtų 9*8*7*6*5*4*3*2*1=362880.
Beje, tokios sandaugos yra vadinamos FAKTORIALAIS, ir rašomos: 9! = 362880; 3! = 6.
Todėl uždavinio sprendimas gali būti pateiktas taip:
9! / (3! * 2!)=38240.
O štai tikimybę apskaičiavote PUIKIAI 🙂
Rasa, 2017-05-19 08:41:38
30 240 🙂 ne 38 240 🙂
Giedrius, 2017-05-19 10:29:03
Atsiprašau už tai, kad man lėtai “daeina” :), bet norėjau pasitikslinti. Norėdami surasti kiek yra viso įmanomų unikalių derinių, jeigu elementai žodyje ar skaičiuje kartojasi, tai visų įmanomų variantų skaičių, kuris apskaičiuojamas faktorialu (kaip buvo parodyta), daliname iš sandaugos tų elementų faktorialų, kurie kartojasi, ir faktorialas tų pasikartojančių elementų yra tokio dydžio, kiek kartų tas elementas pasikartoja?
Ar teisingai supratau?
Rasa, 2017-05-19 10:57:02
Giedriui: visus suskaičiavom, dabar tave skaičiuosiu 🙂
Kiek variantų galima padaryt iš tavo vardo?
GIEDRIUS bus 8!/2! tai lygu 20 160;
Ir atsisveikinant su gražia tema tada reikia suskaičiuot, kokia tikimybė, kad traukiant iš tavo vardo penkias raides ir jas dėstant iš eilės, gausim gražų žodį SUDIE
Aš gavau 1/3360
Gal kada Sokolovas patikrins 😛
Giedrius, 2017-05-19 14:48:10
Rasai: Pamoka išmokta 10-kui 🙂 Laikas į pertrauką :))
Vilkas Pilkas, 2017-05-19 15:37:52
Rasai: dar kartą lenkiu galvą prieš tamstą – Salvadoras Dali iš tiesų prikalė nukryžiuotąjį prie trimatės hiperkubo projekcijos.
Prieš porą šimtmečių inkvizitoriai už tai jį būtų sudeginę ant laužo, o dabar pažiūrėkit, lietuviškasis bernardinų tinklaraštis gegužės 22 d., 2016 straipsnyje “Dailininkas. kuris pasiekė ketvirtąją dimensiją” pateikia teiginį, kad “geometrija … tarsi kelias į amžinąjį išsigelbėjimą” sulaukia vienintelio (prieštaraujančio?) komentaro…
Tempora mutantur, nos et mutamur in illis
Vilkas Pilkas, 2017-05-19 15:47:26
Giedriui: skirkite pradžiai 5 minutes autoriaus pasakai:
http://www.matematika.lt/burgis/tikimybiu-teorija/
…apetitas kyla bevalgant.
Simonas M., 2017-05-19 16:08:25
Dalinuosi ir aš įžvalgomis.
Gražu, kai mokinys pamoką išmoksta dešimtukui, bet nemažiau gražu, kai mokytojas išaiškina temą, taip, kad nusipelno dešimtuko už sklandumą. Pavyzdžiui, jei norime suskaičiuoti, keliais būdais galima sudaryti narių seką (kai eilės tvarka svarbi), pateikčiau tokį aiškinimą:
• Išsiaiškinti, keliais būdais galime parinkti pirmą narį, o tada rasti, keliais būdais galime parinkti kiekvieną tolimesnį narį;
• Isitikinti, kad visada tolimesnio nario parinkimų kiekis bus vienodas, nepriklausomai nuo ankstesnių pasirinktų narių;
• Sudauginti gautus rezultatus.
Jei nepraradot dar azarto, galit iš šios temos tokius paspręst:
-
Keliais būdais galima sudaryti lietuvišką automobilio numerį (pirma 3 raidės, po to 3 skaičiai), kuriame simboliai nesikartoja? Kaip žinia, raidės yra angliškos, angliškame alfabete jų yra 26, tačiau iš jų raidės W, X ir Q numeriams nėra tinkamos.
-
Picerijoje galima užsisakyti 12 skirtingų rūšių picų, iš kurių kiekviena gali būti 4 skirtingų dydžių, o šalia picos galima užsisakyti 5 rūšių kokteilius, 4 rūšių sultis ir 3 rūšių limonadus. Kiek skirtingų komplektų (tik pica ir gėrimas) galima užsisakyti?
…Bet aš kažkaip manau, kad šiame skyriuje yra per mažai užsimenama, kas sugalvojo, kad čia turi būti daugyba. Juk matematikoje svarbiausia suprasti procedūrą, kitaip tu turi pilną teisę pareikšti ,,aš šitos temos nesuprantu!” netgi, jei ir taisykles moki. Gal kas paaiškintų nuo pradžių?
Giedrius, 2017-05-19 18:47:23
Vilkui Pilkui: Dėkui. Tikrai vertingos pamokos. Praeitais metais, kai kartu 🙂 su dukra ruošėmės abitūros egzaminams ne vieną kartą šią ir kitas video pamokėles peržiūrėjome. Tikrai padėjo. Buvau ir jos gimnazijos mokytojams rekomendavęs. Atrodo, įsiklausė, nes buvo pranešę visiems tos laidos abiturientams apie šį tinklapį.
Dukra matematika abitūroje išlaikė visai neblogai, bet daugiausia neaiškumų ko gero liko kombinatorikoje. Dabar sūnus penktokas. Ruošiuosi jo artėjančiai abitūrai 🙂 Ir kaimynų berniukas – šeštokas vis užbėga su matematikos uždaviniais, nes tėveliai jau nebegali padėti. Tai tenka lavintis papildomai 🙂
Sokolovas, 2017-05-19 21:20:47
Simonui M:
Dėl pirmo uždavinio: Ne “trys skaičiai”, o trys SKAITMENYS.
Matematikas turi itin atidžiai vartoti sąvokas.
Dėl klausimo “kodėl daugyba?”
Pavyzdžiui, pirmą elementą (tarkim, pirmąjį patiekalą), renkamės iš aibės A={a, b, c, d}. Antrą elementą (pvz, antrąjį patiekalą)- iš aibės B={x, y, z}.
Keliais būdais galima papietauti?
Gauname aibę:
P={{a,x}, {a,y},{a,z}, {b,x}, {b,y}, {b,z}, {c,x},{c,y},{c,z}, {d,x}, {d,y}, {d,z}}
Pietų komplektų gavome 12= 4*3. Manau, jog kiekvienas suvoks, kodėl reikia dauginti. Nes kiekvienam pirmos aibės elementui galima priskirti bet kurį kitos aibės elementą. Jei pirmoj aibėj n elementų, antroje- m elementų, o mes renkamės pirmos aibės elementą IR antros aibės elementą, tai pasirinkimo galimybių (nesutvarkytų rinkinių {a,x}…) yra n*m.
P.S. Dar aštuntoką galima mokyti spręst uždavinį, pvz, _”susitiko 12 vaikų, jie keičiasi dovanėlėmis, kiek yra dovanėlių? 12*11=132″. Tai yra įžanga į kombinatoriką….
Burgis, 2017-05-20 20:18:23
Kur dingo komentarai?…
Rasa, 2017-05-20 21:05:30
Nu… Dingo! O aš jau buvau beveik nusiteikus kombinatoriką eit mokytis… 😀
Nes vakar kaime labai gerai išsprendžiau tikimybių uždavinį, kurį pati sau sugalvojau 🙂 Parvežėm su žentu toną trąšų, reik kibirais sunešt į kluoną, nes priekaba nuomota. Ir sprendžiu pati sau: kokia tikimybė, kad aš negausiu galo ir abu sunešim tą gėrį? 🙂 (nes trąšos ekologiškos) Bet kadangi tikimybė sau buvo priimtina tik vieną- imi ir neši, tai be klaidų ir išsisprendė… 🙂
Sokolovas, 2017-05-20 21:54:57
VĖL INKVIZICIJA LAUŽĄ KŪRENA
Gerb.Burgiui.
Matyt yra jėgų, talkinančių Vanagams-reformatoriams-griovėjams…
Nepatinka kai kam matematikos žinių sklaida, pirmieji žmonių pasisekimai, diskusijos…Netikiu, jog “dingo atsitiktinai”..
Gerb. Burgio portale nuolat kritikuojami tie griovėjai. Ir juk yra už ką ! Kaip jie pateikia savo vizijas-“mes nutarėme, mes dar svarstome…”. Kas tie “mes”? Korumpuotų bendrininkų saujelė?
NEC, su kuriuo beviltiška susikalbėt.. Aštuntokų standartizuotas testas šiemet slepiamas. Matyt dėl to, jog pernai jame iškilo “Gudyno trikampis”, kurį “žymus matematikas” gynė spaudoj…
Geriausia -nuslėpt.
Dar geriau (versija),- užgniaužti mokslinę mintį. Apie paraleles su inkvizicija jau esu rašęs..
Visi regime, kas vyksta…Tylime…
Burgis, 2017-05-21 08:52:21
Mistika ir tiek… Kur tie komentarai? Buvo dingę, buvo pasirodę, vėl dingo…
Sokolovas, 2017-05-21 09:13:21
Gerb.Burgiui:
Nėra mistikos…Yra nepažintų reiškinių…:)
Burgis, 2017-05-21 09:57:30
Sokolovui: va, veikia!