KL Nr. 7: Gauso metodas – paprasta ir patogu / Burgis.lt

Išspręsime tiesinių lygčių sistemą. To moko ir mokykloje, ir universitetuose, bet gal rasi kai ką, kas tau patiks?

Štai pradinė sistema:

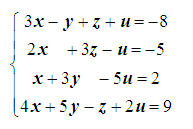
Pirmas „gausiškas“ veiksmas – kam mums tie kintamieji, dirbkime tik su skaičiais! Pasidarysime koeficientų prie kintamųjų ir laisvųjų narių lentelę (matricą). Įsidėmėkite, kad nuo lentelės bet kuriame sprendimo žingsnyje labai lengvai galima grįžti prie lygčių sistemos – užtenka surašyti kintamuosius, lygybės ir sistemos ženklus. Žinoma, gausime jau modifikuotą (pakeistą) lygčių sistemą, bet ji bus ekvivalenti (turinti tokius pat sprendinius) pradinei.

Štai Gauso matrica:

Dabar tai matricai (suprask – lygčių sistemnai) taikysime keturias ir tik keturias paprastas procedūras, taisykles:

**1. Veiksmai atliekami tik su eilutėmis.

Bet kurias eilutes galima sukeisti vietomis (žinoma, juk ir lygtis sistemoje galima keisti vietomis!)
Bet kurią eilutę galima padauginti iš bet kokio skaičiaus.
Bet kurią eilutę galima padauginti iš bet kokio skaičiaus ir pridėti prie kitos eilutės (eilutė, kurią dauginame, išlieka nepakitusi).**

Pradedame! Susikaupkite, iškart atliksime keturis veiksmus:

Pirmąją eilutę sukeisime vietomis su trečiąja.
Po to pirmąją (buvusią trečiąją) eilutę padauginsime iš (–2) ir pridėsime prie antrosios eilutės.
Pirmąją eilutę padauginsime iš (–3) ir pridėsime prie trečiosios eilutės.
Pirmąją eilutę padauginsime iš (–4) ir pridėsime prie ketvirtosios eilutės.

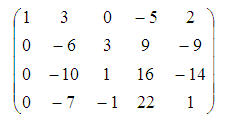
Dabar antrąją eilutę padauginsime iš (–1) ir pridėsime prie ketvirtosios eilutės; po to antrąją eilutę padalysime iš (–3):

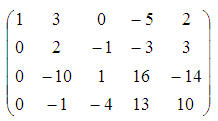
Antrąją eilutę padauginsime iš 5 ir pridėsime prie trečiosios; antrąją eilutę sukeisime vietomis su ketvirtąja. Ar jau aiškėja, kokio tikslo siekiame?

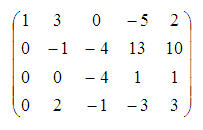
Antrąją eilutę padauginsime iš 2 ir pridėsime prie ketvirtosios; po to antrąją eilutę padauginsime iš (–1):

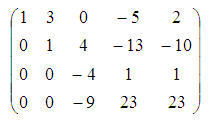
Trečiąją eilutę padauginkime iš (–2) ir pridėkime prie ketvirtosios; po to šias dvi eilutes sukeiskime vietomis:

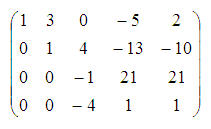
Trečiąją eilutę padauginkime iš (–4) ir pridėkime prie ketvirtosios; po to ketvirtąją eilutę padalykime iš (–83):

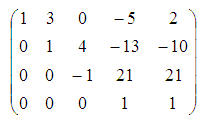
Daugelyje vadovėlių rasite, kad Gauso metodu sistemą jau išsprendėme – dabar laikas grįžti prie kintamųjų ir iš ketvirtosios lygties gauti vieną atsakymą. Bet mes nesustosime! Dabar patys išsiaiškinkite, ką padarėme su matricos eilutėmis (sufleruojame: žiūrėkite „iš apačios aukštyn“):

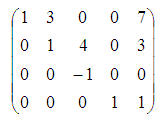
Dar du-trys panašūs veiksmai ir gauname tokią matricą:

Sistemos sprendiniai – paskutiniame stulpelyje!

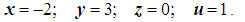
Atsakymai

Mantas, 2009-01-26 12:29:48

Sprendžiame, tai sprendžiame. Bet koks pritaikymas gyvenime?

Burgis, 2009-01-26 12:33:31

Mantui: receptus sudarinėsite, lėšas skirstysite, keliones organizuosite – šimtus darbų dirbant galima sudaryti ir spręsti sistemas…

Raimundas Zabarauskas, 2009-01-26 13:26:07

Receptus? Lėšas ir keliones? Šimtus darbų dirbant galima apsieiti be matricų ir lygčių sistemų…

Mantui: proto mankšta, matematikos dantračių aiškesnis suvokimas, galų gale, jais grožėjimasis.

Mantas, 2009-01-26 14:35:52

Proto mankšta gera, su šituo aš sutinku. Šiaip ir pats esu matematikos mėgėjas, bet va vis tiek retkarčiais pasigendu prasmės.

matematikos mokytoja, 2009-01-26 17:28:13

Mantui. Mano dukra šiandien po matematikos kontrolinio atsiuntė žinutę: “… pritrūko laiko ir smegenų.” 🙂 Kad suprastum matematikos prasmę kartais trūksta antrojo komponento 🙂

Mantas, 2009-01-26 18:20:45

@matematikos mokytoja

Aš suprantu, kad kažkokių minimalių matematikos žinių reikia, suprantu jų prasmę. Bet jūs paaiškinkit, koks man tikslas mokytis visas tas matricas, Gausus, Kramerius, diferencialus ir visus kitus sutvėrimus, kuriuos aš po keleto mėnesio vis tiek užmiršiu. Koks man jų pritaikymas gyvenime?

GL, 2009-01-26 18:48:15

Na matricu ir diferencialu pritaikymu apstu visur: statistikoje, finansuose, inzinerijoje, (modernioje) biologijoje, (modernioje) psichologijoje, fizikoj, chemijoj, neuromoksle, marketinge – manau butu sunku rasti sriti (na isskyrus humanitarines ir meno), kur ju nera…

Bet va mokytis spresti lygtis ranka – sutinku, tik gera proto manksta (na ir aisku, pradedantiesiems tai kartais padeda geriau suprasti tu matricu ar ko esme). Bet kiek zinau visuose rimtuose pritaikymuose niekas ranka neskaiciuoja – naudojami paketai (tokie kaip MatLab, SPSS, etc.) kurie (be abejo remdamiesi tais paciais Gausais/Krameriais ar kartais efektyvesniais algoritmais) atlieka skaiciavimus ir duoda rezultata.

matematikos mokytoja, 2009-01-26 18:49:07

Tai ir nesimokykit. Kas Jus verčia tai daryti? Su “minimaliomis” matematikos žiniomis Jūsų paslaugoms profesinės mokyklos. Ten Jus mokys tik tų dalykų, kurių reiks gyvenime.

matematikos mokytoja, 2009-01-26 18:54:23

Prieš tai rašytas komentaras – skirtas Mantui.

GL. Gal nereikia taip kategoriškai išmesti humanitarinės ir meno sričių. Fantastinėje literatūroje tikrai galima sutikti ir matricą, ir diferencialą, ir integralą. Gal dėlto šią literatūrą labiau mėgsta berniukai (vyrai) negu mergaitės (moterys).

GL, 2009-01-26 19:01:12

O labai gaila, kad tos profesines mokyklos neturi tokios reputacijos, kokia turetu tureti (ir kokia pelnytai turi vakaruose).

Pas mus viska megstama supaprastinti i viena dimensija – jeigu eini i profesine, reiskia tu blogesnis, nes negali studijuoti universitete…

Kai (jei) sitai susitvarkys, universitetuose bus kur kas maziau zmoniu, kurie kur kas geriau tiktu kolegijoms ar profesinems (ir ten galetu mokytis to, kas jiems idomu, ir ramiai bei neretai pasiturinciai gyventi…)

Mantas, 2009-01-26 19:36:40

@GL

Na maždaug suprantu. Bet vis tiek, išmokstu aš tuos daiktus spręst, išlaikau egzaminą, po metų jau vargiai ką sugebu su jais padaryt. Vis tiek man tai atrodo beprasmiška.

@matematikos mokytoja

Aš jūsų neklausiau, ar man verta mokytis, aš jūsų klausiu, kokia man nauda gyvenime iš to, kad aš išmokstu tuos Gausus, Kremerius ir visus kitus?

Iš jūsų atsakymo iš viso galima susidaryt tokią nuomonę, kad gyvenime naudingų dalykų galima išmokt tik profkėse, reškia, kad universitetuose mums kiša niekam nereikalingą gyvenime nepritaikomą informaciją (nors realiai, tai beveik taip ir yra). Bet visgi tarp daugybės beprasmės informacijos, mes gauname ir daug naudingų žinių.

O tą pasiūlymą stot į profkę, atmesiu. Nesiruošiu išeit iš universiteto.

Ir visgi pakartosiu savo klausimą dar kartą, kokia man nauda gyvenime iš aukštosios matematikos, norėčiau kažko konkretaus?

GL, 2009-01-26 19:46:25

Pirmiausiai pasakyk, ka konkreciai nori daryti – kurioje srityje ar pan., gal tada padesiu…

Nes, kaip minejau, matematiniai metodai yra svarbus irankis daugelyje sriciu (na OK, zinau, matematikos idealistai tokio pasakymo nekencia, bet ka padarysi… visiems neitiksi :))

O siaip: manau reiketu paskelbti zodi “profke” kaip necenzurini ir nevartotina… Is viso as jas pervardinciau (pvz. Olandijoje jos vadinamos Hogeschool, Vokietijoje – Fachhochschule). Gal tada ilgainiui pageres ju prestizas.. 🙂

matematikos mokytoja, 2009-01-26 20:40:04

Mantai, aš Vilniaus universitete 5 metus mokiausi TOKIOS matematikos, kurios mokant mokinius vidurinėje mokykloje dar nė karto per 25 metus neprireikė. Bet dar nė karto nebuvo taip, kad mano mokinys mokėtų daugiau negu aš (kol jis dar mokinys). KTUG nedirbau, nežinau gal ten būtų buvę kitaip. Pagal Jūsų logiką aš universitete turėjau mokytis tik vidurinės mokyklos kurso, nes gi kitko nereikia. Ir ką aš po tokių “studijų” galėčiau pasakyti tokiam mokiniui kaip GL?

Lietuvos aukštasis mokslas yra didžiulėje bėdoje, jei net tokie stropūs studentai kaip Jūs neskiriate universitetinio išsilavinimo nuo profesinio. Universitete mokoma metodologijos, t.y. universalių tyrimų ir analizės metodų, principų; matematika (kaip ir filosofija…) ir yra vienas iš jų. Tuo universitetas ir turėtų skirtis nuo kolegijos. Nereikia sakyti, kad KTU nėra praktinių disciplinų. Nepatikėsiu. Tikrai žinau, kad taip nėra, pusė mano klasiokų yra baigę šį universitetą.

Jūsų didžiai nuostabai pasakysiu, kad matematinius metodus taiko ir filologai, bet ne tie kurie moko vaikus gramatikos, o mokslininkai. Taip, kad bet kuriam mokslui matematika reikalinga, kaip universalus pasaulio pažinimo metodas.

Irid, 2009-01-26 22:34:19

Pagal Manto pamąstymus išeitų, kad ir Ferrari gyvenime neturi pritaikymo. Dešimt metų juodai dirbsi, kol nusipirksi, o paskui – į kaimą pas bobutę vieškeliu nenuvažiuosi, Maksimos aikštelėje nepaliksi, benzino ryja daug, uošvienė ant galinės sėdynės netelpa. Praktiškai niekam netinkamas grabas.

Adomas, 2009-01-27 01:23:37

To Irid

Dėl ferario – bet juk taip ir yra! Taip, kaip parašėte! Taip, ir uošvienė netelpa, ir visi ko gero lietuviai, kurie turėjo ferarius, jų nebeturi (na, ten Ranga IV ar pan.). Viešpatie, juk tai snobizmas. Nieko prieš, turi pinigų ir snobišką prigimtį – pirk ferarį. Čia toks pat snobizmas, kaip ir su, pvz., kokiu garsiu dailininku – paprašyk kokios mokyklos (gal prie meno) mokinuko, kad nupieštų kokį smuikininką a la Šagalas, duodu kepurę prikakoti, kad ferario snobas to piešinio nepriims už tikrą pinigą, aišku, jei prieš tai pasakysi, va, čia Šagalas (o kas jis toks?..). Mes dažnai perkam vardą, o ne prekę. Juk marškinėliai su užrašu per visą krūtinę BOSS kainuos brangiau nei su užrašu ZOSĖ. Sorry, bet tai su matematika neturi nieko bendro. O šiaip, baigiau sustiprintą matematiką vidurinėje, truputį matricų teko ragauti Maskvoje, po to baigiau su medicina susijusius mokslus Lietuvoje, bet kažin kodėl iki šiol sapnuoju (bent kartą per mėnesį), kad niekaip negaliu išlaikyti matematikos egzamino. Velniaižin ką Froidas su Jungu pasakytų…

O juk jau 20 metų praėjo.

Tiesa, diferencialų ir kitų likusių šposų gyvenime panaudoti neteko.

VR6, 2009-01-27 03:37:12

Mano nuomone matricos, linijinis programavimas, yra viena is elegantiskiausiu ir praktiskiausiu matematikos sriciu. Nors ir dirbu su konkreciais skaiciais, vien tai kad suvokiu matricas ir kartais panaudoju ju principus modeliuodamas man labai palengvina gyvenima, ir padeda pasiekti rezultatu efektyviu budu.

Tiesa yra tai, kad labai daug mano kolegu, nezino tu principu ir ju nesinaudoja. As tas matricas ismokau gerai, ir jos man jau praverte simtus kartu, nors niekada darbe matricos ir linijinis programavimas neminimas.

Man matematika tai kaip .. muzika. O tiems kurie sako, kad neimanoma panaudoti matricu, as galiu pasakyti tiktai, kad yra itin daug vietu kur galima panaudoti gyvenime. klausimas ar is tikruju visi moka pritaikyti tai ko taip gerai ir neismoko.

Raimundas Zabarauskas, 2009-01-27 06:48:29

Mantai, sportuoji ne tam, kad laimėtum Olimpinį medalį. Galandi įrankius iš anksto nežinodamas, ką išdroši iš savo gyvenimo medžio.

Aukštasis mokslas turėtų būti labiau „abstraktus“, ne–vien–būsimai–profesijai–skirtas, negu profesinis mokymas.

Baigęs fiziką pamiršau ir matricas, ir tenzorius, ir erdvinius integralus. Tačiau praplėstas mąstymas vėliau smarkai pravertė.

Atsimenate Džonataną Livingstoną Žuvėdrą? Pratybomis išmoktama skrist kiaurai sieną, tad verčiau atsikratykit Pusryčiautojų Būrio logikos.

Liutauras, 2009-01-27 07:58:51

Ačiū! Arba buvau visai pamiršęs, arba matricų dalis neužstrigo. O praktinis pritaikymas labai paprastas – pavyzdžiui, prieš pora savaičių “tradiciniu” būdu turėjau spręsti 4 kintamųjų lygtį, galvodamas apie naująją apmokestinimo sistemą (kintamieji – sveikatos draudimas, socialinis draudimas, pajamų mokestis, sąnaudos)

Kęstutis, 2009-01-27 10:20:16

Sprendžiame, tai sprendžiame. Bet koks pritaikymas gyvenime?

Dalis iš čia rašančių yra mokytojai. Seni patyrę matematikos vilkai, galėję valgyti tą patiekalą be užkandos. Bet buvo kitaip, jie valgė gardžiuodamiesi, patikėk, mačiau aš tas akis prieš 20 metų. Gal kada nors gyvenime pagausi besidominčio vaiko žvilgsnį. Atkreip dėmesį, paaukok jam savo trupinį, sudėk skaičius taip, kaip jam nesudeda jo vadovėlis ar jo matematikos mokytojas. Gal būt ateis po 10 metų, gatvėje sustabdys ir pasakys: ačių, Jūs manę išmokėte matematikos. O buvo … viso labo keli skaičiai. Patikėk, teko susidurti, nepakartojamas jausmas.

GZ, 2009-01-27 12:18:57

Man matematikos po universiteto, deja, neprireikė. O mokytis ją labai patiko. Kaip ir fiziką, ir psichologiją, ir kitus aukštojo mokslo siūlomus (čia pagražinau…) dalykus. Visgi iki šiol stebiuosi, kiek daug nepalietėm mano specialybėje (informatikoje), pločio prasme. Gilyn galima išsistudijuot jau pačiam studentui, o vat apie koncepcijas tai būtų neblogai išgirst mokykloje.

Manto klausimas, nukreiptas į matematiką, gali būti lengvai “persuktas” į kitus mokslus (žinote, kodėl dangus mėlynas ? žinau tik, kad mokėmes kvantinėje fizikoje, bet atsakymo neprisiminsiu… fiziką kasėme tikrai giliai…)

Tai man šioje temoje visada labai padeda sporto analogija. Jei būčiau neištempęs tų krūvos mokslų universitete (o pasidavėlių buvo net ketvirtis kurso per vienus metus !), kaip gi galėčiau darbdaviui garantuoti, kad susitvarkysiu su _visais_ man teikiamais darbais ? O darbai iki šiol ateina įvairiausi, ir tuo džiaugiuosi. Kitaip būtų nuobodu gyventi.

Raimundai, o apie Pusryčiautojų Būrio logiką dar nesimokiau. Mielai apsišviesčiau.

Klausimai…, 2009-01-27 13:24:06

Dangus mėlynas, nes trumpųjų bangos ilgių šviesa daug stipriau sugeriama atmosferoje esančių molekulių, nei ilgųjų bangų šviesa. Tada ji vėl išspinduliuojama, kai tos molekulės grįžta į nesužadinta būseną (bet jau visomis kryptimis). Tai yra vadinamoji Relėjaus sklaida.

Vainius, 2009-01-27 17:11:03

Tik vat įdomu kodėl trumpųjų bangos ilgių šviesa daug stipriau sugeriama? Energijų skirtumas tarp elektronų būsenų labiau atitinką trumpos bangos ilgio energiją ir dėl to lengviau įvyksta sužadinimas? Ar kas čia vyksta? 🙂

Vainius, 2009-01-27 17:55:18

Antras klausimas (nors čia galbūt reikėtų rašyt į kokį sandėliuką, bet kad jau sudomino..). Tarkim keliauja šviesa per atmosferą, ir tą mėlyną ir šiaip trumpesnę vis sugeria ir išspinduliuoja, tai ar netūrėtų kaip tik dangus raudonas nuo to būti? Juk gaunas, kad raudono bangos ilgio fotonai iki mūsų beveik visi atkeliauja, o labiau link mėlyno sugėrus išspinduliuojamas pavyzdžiui į priešingą kryptį ir gaunas, kad tik koks trečdalis pasiekia?

ST, 2009-01-29 04:55:32

As spresciau kitu budu si uzdavini. 1. sudaryciau 4×4, 4×1 ir 4×1 matricas, 2. rasciau ^-1 pirmosios matricos ir padauginciau rezultata is treciosios matricos.

Darius, 2009-01-29 14:34:30

@Klausimai

Na, ne visai del oro molekuliu. Pamenu, kad priezastis yra dulkes atmosferoje. Ir priezastis greiciau – elementari difrakcija… Jei oras butu idealiai svarus, dangus butu juodas it menulyje.

Buvo pries mazdaug metus Vilniuje kazkoks italu fizikas surenges sviesos sou: nuo vaivorykstes iki lazeriu ))) Labai ispudinga, iki siol pamenu

Vainius, 2009-02-11 04:57:03

Nesvarbu, kad tema jau, rodos, užmiršta, reikia bent vieno klausimo su PAČIA tema susijusio, o galų gale jis ir iškilo (gal ir kvailas..):

O kaip būtų galima įrodyt, kad tokie sprendiniai yra unikalūs? T.y. truputį kitaip atliekant operacijas su eilutėmis, kad gauti tą galinę formą, nesigautų kitas sprendinių ketvertas.

GL, 2009-02-16 18:47:12

Na, jeigu tiesiniu lygciu sistema turi bent 2 sprendinius, nesunku irodyti, kad ju yra begalybe.

tarkim ir yra 2 skirtingi sprendiniai, tada p+(1-p) bus taip pat…

GL, 2009-02-16 18:49:09

oops, HTML’as “suvalge” mano sprendinius. :]

Norejau pasakyti, kad jeigu {a1,…,an} ir {b1,…,bn} sprendiniai, tada p{a1,…,an}+(1-p){b1,…,bn} taip pat…

Burgis, 2009-02-16 19:22:23

GL: Gediminai, prašyčiau negąsdinti lankytojų…

GL, 2009-02-16 19:31:20

Sorry, as tik norejau pasitikrinti, ar dar sugebu irodyti paprastus dalykus matematikoje… (ir atsakyti i Vainiaus klausima) 😉

matematika…, 2010-01-10 19:37:18

arba as kvaila, arba as nieko nesuprantu situose gauso metoduose, nejaugi niekas nesugeba padaryti normalaus matricu tinklapio, kur butu viskas detaliai isaiskinta, kodel dauginame is -2, o ne is kitu skaiciu ir t.t. jei jau destytojams nepakanka laiko isaiskinti temas tai bent internete butu smulkiai tai aiskinama. antra diena sedziu prie situ matricu ir niekaip nesauprantu, tai tuomet kaip islaikyti egzaminus ir uz ka as universitetui moku pinigus? kad per paskaitas pakalbeciau kas politikoje naujo ir siai paskaitai skiriama tiek pat kreditu kaip ir rimtoms paskaitoms, tokioms kaip taikomoji matematika ar mikroekonomika…

Burgis, 2010-01-10 20:23:25

matematika: geriau parašykite man el. paštu, atsiųskite tą sistemą – žingsnis po žingsnio išspręsiu, gal bus aiškiau.

Rokas, 2010-09-28 20:44:51

Sveiki, gal galite man padėti išspręsti vieną lygčių sistemą Gauso metodu? 🙂 Niekaip nepavyksta, nežinau ką ne taip darau…

Burgis, 2010-09-28 21:29:30

Rokui: atsiųskite el.paštu arba parašykite čia – išspręsiu.

Justas, 2010-09-29 17:40:42

As turiu sistema bet neisivaizduoju kaip issprest:

x1+2×2+3×3+4×4=5,

7×1+14×2+21×3+28×4=35,

8×1+16×2+24×3+32×4=40,

3×1+6×2+9×3+12×4=15

Tai matrica kaip suprantu tokia:

1 2 3 4 5

7 14 21 28 35

8 16 24 32 40

3 6 9 12 15

O kaip toliau pertvarkyti gal kas paaiskins ir kodel?

Justas, 2010-09-29 19:05:58

Tai va issprendziau tik pasakykit ar gerai

gavosi kad x1+x2+x3+x4=5 tai taip iseina kad be galo daug sprendiniu ar as klystu?

Burgis, 2010-09-29 21:11:52

Justui: taip, Jūs teisus, juk visos lygtys vienodos! Suprastinus, žinoma…

Powl, 2010-09-30 19:43:41

Gyvenime tai ju 1% naudos mokinuosi kolegijoje elektriku, ir visai nesuprantu kam taip ziauria ten reikalinga tokia matematika, kad net iki matricu, as suprantu ten kur zmones mokosi branduoline fizika ir panasias specialybes tj va ten tai tikrai reikalinga, o va kam elektros energetikams to reikia nepagaunu kampo, manau jiem labiau yra reikalinga braizyba ir fizika, bet ne matematika, nor ir apie fizika ta pati galiu papasakot x) zodziu zmogus turi dienoj 5 paskaitas, pareini namo pavarges, tai jus pasukit galvas koks normalus zmogus nores dar ziuret i tas knygas ar visai bent mokintis?? kai parvarai namo 7 valanda + valgai 1valanda jau 8h !!! o juk ryt vel 8h keltis !!! ka mes androidai kyborgai???? tie kurie mokinasi nuo sena tai jau pasisvente ant mokslu ir daugiau nieko daugiau gyvenime nemato tik mokslus nes kitur nepritampa. Zinau toki dalyka, kad musu jaunimas isvaziaves i usieni mokintis daznai buna perkeliamas 1-3 klases aukstyn! nes pas kus mokymo tempas per sunkus + 12 metu, jums neatrodo kad tai kazkokia nesamone? Viska kopijuojame nuo ES tai ko i mokslu taip pat neziurime nuo kitu saliu, musu jaunimas Lietuvoje uzsienyje yra labiausiai skaitomas priplaukusiu nes mes nuo tu mokslu degraduojame, o tai del tos krizes dabar mes privalome mokintis TIKRAI nes tokioj saly bus sunku mum + klasiokai tampa musu konkurentais man tai nepatinka. Moralo pagr tema butu tokia kad maziau tu matricu ant tokiu specialybiu kaip Elektronika ir t.t as esu studentas istojes i tokio tipo mokykla ir nenoriu susigadinti savo normalaus nuosavo gyvenimo per moslus is kuriu man tik 3% naudos sprendziant kryziazodzius xD

Vytenis, 2010-09-30 19:57:31

Kam mum tu matricu? Jei renkiesi specialybe tai reikia daugiau i jos struktura mokomaja medziaga taikyti, nei i tas matricas, as vyrukas klybinis ir tikrai nezadu svaistyt savo jaunystes tokiom paikiom vienkartinem nesamonem

Rokas, 2010-10-03 22:05:05

x1+2×1+8×3+x4-2×5=0

-2×2-6×3-6×4=0

2×1+6×2+22×3+8×4-4×5=0

-x1-6×2-20×3-13×4+2×5=0

rasti sistemos bendrąjį sprendinį.

Čia kintamieji x1,x2,x3,x4,x5 🙂

Rokas, 2010-10-03 22:06:14

ui, klaidą įvėliau sąlygoj… Pirma eilutė x1+2×2+8×3+x4-2×5=0

profkis, 2010-12-07 20:54:31

„…Vytenis, Rugsėjo 30 19:57 #

teisybę sakai, kam tie mokslai, geriau jau į kokią “statybinę” profkę ir iš karto į stroikes juodadarbiu…

Ignas, 2011-09-08 11:53:30

Programėlė, galinti pagelbėti su Gauso metodu– pasitikrinti ar gerai padarėte. Keturi nežinomieji ir keturios lygtys. 15 eilutėje atsakymas. Ne visiškai baigta, bet savo darbą atlieka puikiai

Paulius, 2011-10-27 15:00:22

Sveiki as nesuprantu kodel yra dauginama is -2 ? Gal kas galetumet paaiskinti? buciau dekingas.

fernanda, 2011-11-29 11:13:38

Sveiki, galit pasikinti kaip jus nusprendziat is kokia skaiciaus reikia dalinti ar dauginti? visiskai nesuprantu as gauso metodo…o reikia ismokti

martis, 2011-12-06 23:32:19

Sveiki, turiu beda niekaip nesuprantu situ matricu, ir turiu issprest uzduoti atsiskaitymui, gal galetu kas padeti? dekui

Artūras, 2012-11-03 20:47:43

Sveiki. gal galite padėti? reikia Gauso metodu išspręsti duotą lygtį . (jei nesunku – nuosekliai) Dėkui

3 -2 6 = 1

2 11 -9 = -8

1 -7 -3 = -3

Lukas, 2013-02-06 16:13:55

6y+3=20

Justina, 2014-11-14 13:54:39

padekite issprest gauso metodu

x1+3×2+2×3+4×4=10

2×2+x1+3×4=6

x1+x2+x3+x4=4

Gintarė, 2015-11-17 22:14:20

O čia kartais ne Žordano metodas? 🙂

Tomas, 2017-09-07 00:45:06

Ech, ką tik įstojau į VU ir pradėjau šito mokintis. Kad žinotumėte, kaip palengvinote gyvenimą! 😀

Aidas, 2020-05-26 03:23:29

Pragyvenau virš 40 metų. Iki šiol neprireikė, ir labai abejoju, kad prireiks