Internete radau gražų geometrinį uždavinį:
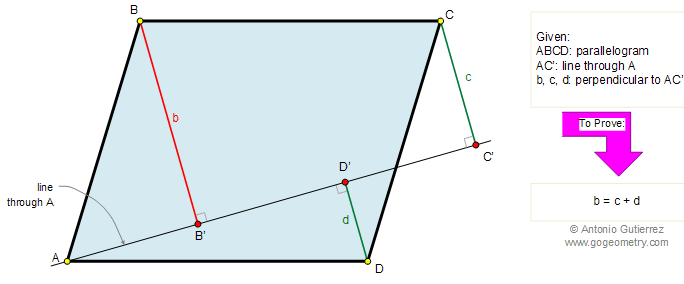
Sprendimą pasiūlysite jūs, o man patiko, kad šiuo pavyzdžiu galima pademonstruoti principą, kurį vadinu “ribiniu” arba “pratęsk iki begalybės”. Apie jį šioje svetainėje jau rašiau (surask apie Renatą ir kavą su brendžiu…), o dabar pažiūrėkite: kas bus, jei 1) tiesė per A eis ir per C (“atsitiktinai” sutaps su įstrižaine…); 2) tiesė per A eis ir per D (“atsitiktiniai” sutaps su karštine…). Tais ribiniais įrodinėjamoji lygybė nekelia abejonių (atsiprašau tik dėl savo negebėjimo nubrėžti statmenų linijų…):
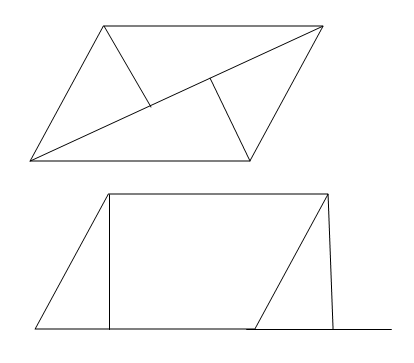
Tie du atvejai įkvepia pasitikėjimo įrodinėjant ir pateiktuoju atveju…
Jau įrodėte?
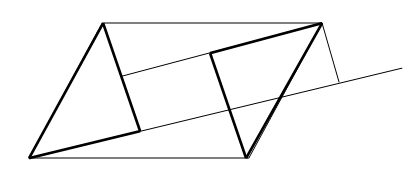
Štai mano įrodymas (paryškinti du lygūs statieji trikampiai):
Atsakymai
Vainius, 2009-02-09 21:25:08
Pildom brėžinį tiese BE, lygiagrečia AD`, ir tiese EC, statmena BE.
O toliau jau paprasta, tik niuru. EC = d, nes BC=AD ir kampas EBC = DAD`, ir kadangi figūra B`BEC` stačiakampis b = c + d.
Vainius, 2009-02-09 21:36:40
O tas “ribinis” principas, kur norėjot parodyt, tai visai rimtas dalykas yra, kai reikia patikrint ar formulė bent panaši į teisingą, arba rinktis tarp kelių formulių. MIT open course yra toks kursas Street fighting mathematics, ir ten extreme cases method yra atskira paskaita skirta. Ten ten šituo principu remiantis randa (atspėja?) įvairiausias formules: nuo elipsės ploto, harmoninių svyravimų periodo, integralo e^(-ax^2) iki nupjautainės piramidės ploto. 🙂
Burgis, 2009-02-09 22:08:31
Puiku, Gerb. Vainiau, bet dar leisime rasti ir kitų įrodymų (turiu lyg ir truputėlį aiškesnį…).
Taip, ribinis principas tikrai naudingas, šioje svetainėje rašyta ir apie Monty Hall uždavinį – imkite vietoj 3 durų bent 10, ir viskas tampa aišku…
GL, 2009-02-09 22:22:43
Grazu! 🙂
Sprendima desimcia zodziu butu galima parasyti taip: atpjaukit gabaliuka apacioje, priklijuokit ant virsaus, ir viskas bus aisku 😉
Burgis, 2009-02-09 22:27:18
Na, jūs, fanatikai-matematikai, duokite paprastiems žmonėms pasimėgauti randant sprendimą. Anoks čia dyvas, kad GL išsprendžia tokį uždavinį… :-)))
GL, 2009-02-09 22:38:25
As jo neissprendziau, tik isverciau Vainiaus formalu matematini sprendima i “zmoniu kalba”… 🙂
Raimundas Zabarauskas, 2009-02-10 05:42:18
O aš pasukau brėžinį, kad AC’ taptų X ašimi.
Tada pamačiau, kad b/AB’ = (c+d)/D’C’, nes AB ir CD lygiagrečios ir lygios. Be to, AB’ = D’C’, nes tai tos pačios (tik kitus paslinktos) atkarpos projekcija į X ašį.
Pjaustantysis GL sprendimas grakštesnis. O kuo čia dėti ribiniai atvejai?
Burgis, 2009-02-10 21:42:57
Įdėjau savo sprendimą, bet tegu skaitytojai panagrinėja visus, randa dar geresnių…
Raimundui: dviem mano parodytais atvejais įrodinėjamoji atstumų lygybė yra akivaizdi (nesvarbu gi, kad vienas iš trijų atstumų sutrumpėja iki nuolio…). Tai tikrai padėtų tuo atveju, jei norėtume rasti ryšį tarp atstumų, bet nežinotume, kad dviejų atstumų suma lygi trečiajam atstumui.
Raimundas Zabarauskas, 2009-02-11 05:07:28
Ačiū, supratau. Tik įrašęs savo ankstesnį komentarą, staiga suvokiau, kad b yra atkarpos AB, o c+d – atkarpos CD projekcija į statmeną tiesei AC’ tiesę (tai beveik sutampa ir su Jūsų pasiūlytuoju, ir su GL sprendimu)…