Dabar imkime ir suraskime ryšį tarp trijų jau jums pateiktų temų: eilučių, kompleksinių skaičių ir trigonometrijos („Korepetitoriaus langas Nr. 3“ (KL3), KL4, KL5). Būkite pasirengę pasimėgauti mistiškiausia (bent jau man…) matematikos formule!
Taip, kaip KL3 lange sudarėme sinuso eilutę, padarykime dar dvi eilutes – prireiks visų trijų (visada jos visos pateikiamos formulių rinkiniuose, todėl galima sudaryti pačiam, galima „nusirašyti“):




Ar supratote, kaip išsprendėme? Tai galėtų būti atskira tema…
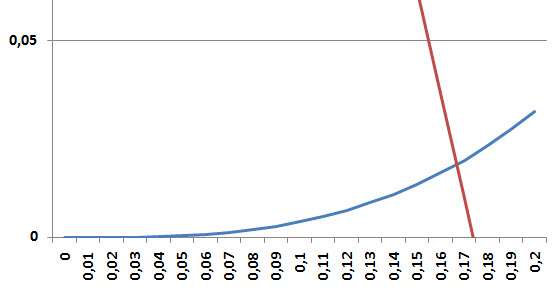
Patikrinkite skaičiuotuvu: sinusas dešimties laipsnių yra 0,1736482.
Manau, kad jau laikas jums ko nors paklausti…
Atsakymai
Vainius, 2009-01-25 19:44:17
Šitas KL labai šaunus! Dabar kad galutinai įsitikint, kad E^iPi + 1 = 0, norėtųsi dar sužinot, kaip sugalvota-išvesta Teiloro eilutė. Ir dar akis truputį kliūva už jau išskleistos alternuojančios eilutės pertvarkymo, visi žinom, kad keičiant dėmenų eiliškumą galima “priversti” ją konverguoti į visai kitą skaičių, tad kodėl šiuo atveju taip neįvyksta?
Burgis, 2009-01-25 19:57:34
Vainiui: atsiprašau, Jūsų klausimų per daug ir jie – erudito klausimai. Nenorėčiau atsakymais “nubaidyti” mažiau pasirengusius, bet trumpai atsakysiu: 1) sudėtingumu labai skiriasi būtinosios ir pakankamosios Teiloro eilutės sąlygos (visai paprasta, kai pradedame taip: tarkime, kad funkcija “teisėtai” išreikšta laipsnine eilute; kokie tada turi būti tos eilutės koeficientai?); 2) čia alternuojančiosios eilutės nariai vietomis nekeičiami, tik pirma išrenkami kas antras, paskui likusieji, bet apskritai “leistinumą” galima įrodyti remiantis absoliučiuoju konvergavimu. Pakaks…