Siūliausi nemokamai mokyti studentus – niekas neužsakė… Tėveliai, seneliai, moksleiviai, studentai – neskubėkite užverti šio lango! Jei tau nesvarbu, neįdomu – pasakyk kaimynei, kuri verkia, kad neturi už ką nusamdyti vaikui korepetitoriaus. Štai aš jos vaiko paslaugoms!
Nežinau, ko jūs nemokate, bet pasirinkau temą, kurią, garantuoju, mūsų šalies švietimo sistema pateikia netinkamai. Parabolė. Kvadratinė lygtis. Kvadratinis trinaris, nelygybė. Mėnesių mėnesius moksleiviai ir studentai (taip, ir studentai!) “zubrija” tokį paprastą dalyką, o paklausk šią svetainę aplankiusio suaugusio žmogaus “Kas yra parabolė?” – pasakys (geriausiu atveju) kas dešimtas…
Kodėl taip yra?
Pirmiausia pažvelkite į šias kreives: viena iš jų – parabolė, kita – hiperbolė. Atskiriate? Netikiu…

Keisčiausia, kad mokykloje “kala” į galvas, jog parabolė gali būti (tik?!) tokia – vienas iš šešių variantų:
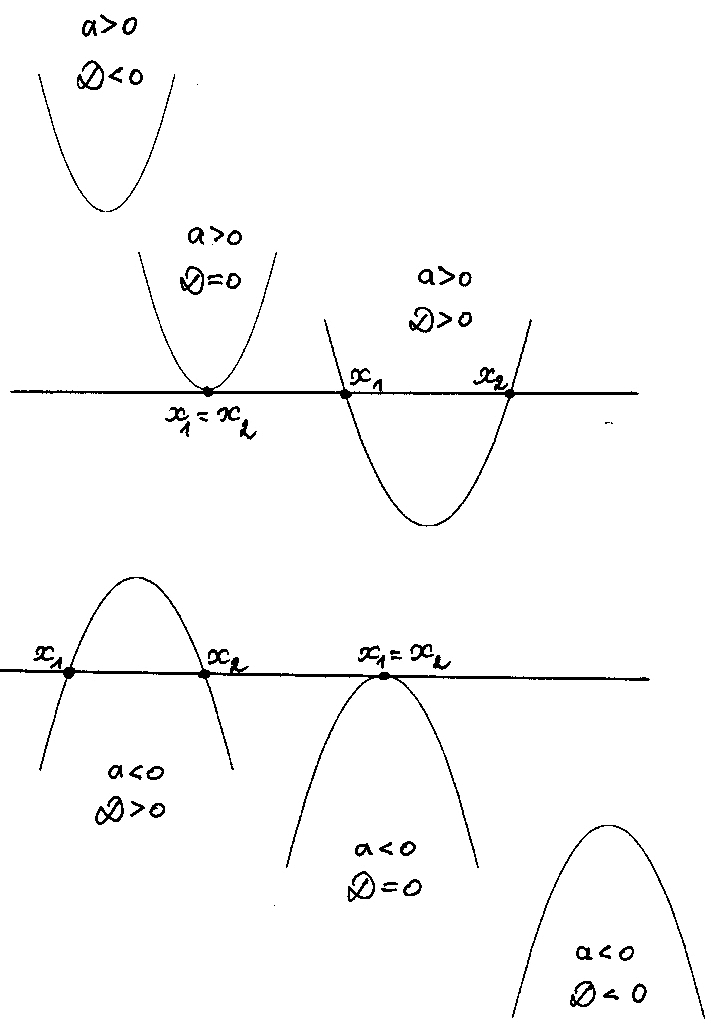
Gera paruoštukė, nesiginčiju. Bet štai universitete (lietuviškame; amerikiečiai tokios kreivės nelaiko funkcijos grafiku…) pasako, kad parabolė yra tokia:
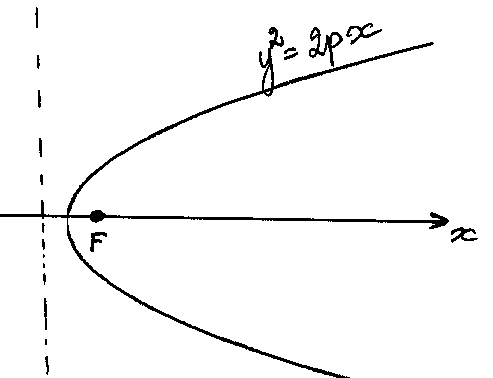
Kas tas F? Kas ta punktyrinė tiesė? Židinys ir direktrisė. Pasidarė aiškiau? Vargu.
Leistų man, aiškinčiau taip:
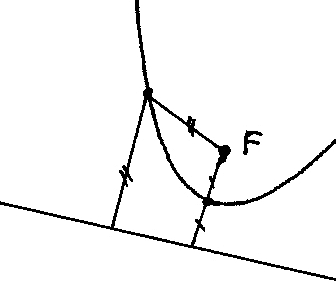
nubrėžk bet kokią tiesę (kodėl horizontalią? kodėl vertikalią? bet kokią!) ir pavadink ją direktrise. Šalia tiesės (bet kur!) padėk tašką ir pavadink jį židiniu (F; todėl, kad anksčiau židinį žmonės vadino “fokusu”!). Dabar dėliok taškus taip, kad jų atstumas nuo direktrisės ir židinio būtų vienodas. Tie taškai ir sudaro parabolę!
Dabar, kai jau žinai esmę, gali grįžti prie to, ko moko mokykloje, bet žiūrėk į viską iškart:
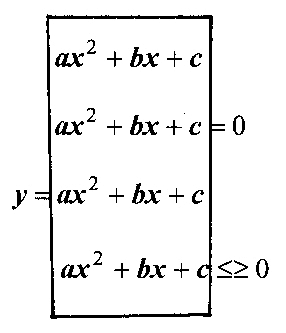
Trinaris, lygtis, funkcija, nelygybės – taip aiškiai susiję dalykai, kad neverta gaišti laiko kiekvieną mokantis atskirai. Bet gal jau gana pirmam kartui?
Pasiūlykite kitą temą!
Atsakymai
Rolandas, 2009-01-21 15:05:31
tai Statistikos departamentas ilgai pagal sena formule (be paklaidos epsilion) skaiciavo BVP, tai jau matyt dabar ir esame kur esame , nes viskas kitaip atrode Europoje kur mums sake, kad jusu augimas leteja nei cia, kur rekiama buvo, kad pas mus nerealus augimas
Burgis, 2009-01-21 15:34:45
Gerb. Rolandai, koks ryšys tarp parabolės ir BVP? Ar Jūs tiesiog pasinaudojote šiuo langu pateikti savo graffiti?
matematikos mokytoja, 2009-01-21 16:26:34
Lietuviškoje mokykloje trečiame paveiksle pavaizduota parabolė irgi nėra funkcijos grafikas.
GL, 2009-01-21 17:06:07
Pirmiausia pažvelkite į šias kreives: viena iš jų – parabolė, kita – hiperbolė. Atskiriate? Netikiu…
O jus galetumete? 🙂
O siaip labai sutinku, ypac del paskutinio paveikslo – form.jpg
Del kitu temu bent man sunku pasakyti – nelabai atsimenu kaip konkreciai kas buvo mokoma… Bet siaip i ta pacia tema – juokinga istrauka is mano pokalbio su broliu:
“zinai, as jau pamirsau daug dalyku, net karta pvz. reikejo isspresti kvadratine lygti, ir galvojau – ar ten ac ar 4ac ar b ar 2b ar 2 ar kaip… 🙂 Vietoj to nuejau i MatLab – ir saknys rastos (na, aisku, po to, susigedijes, nuejau, susiradau formule, ir prisiminiau…)”
o jis man:
“tai kaip nezinai – yra du budai – su diskriminantu, ir be…”
as (confused):
“diskri…? kas cia per daiktas? kam to reikia? juk paprasciausiai yra formule ir viskas…”
Pasirodo is tikruju egzistuoja toks diskri… 🙂 bet visiskai nuosirdziai sakant, as ji buvau visiskai pamirses, ir net dabar nesu isitikines, ar jo tikrai reikia paprasciausiam lygciu sprendimui…
matematikos mokytoja, 2009-01-21 17:38:50
GL. Aš ir B.Burgis labai sėkmingai mokėmės spręsti kvadratines lygtis be jokio diskriminanto. Jis atsirado vėliau. Bet Jūs esate pakankamai jaunas, kad žinotumėte, kas tai yra :). Man tas diskriminantas irgi labai nepatinka. Vaikai nelabai ką suvokdami kaip mantrą kartoja.
F. Ch., 2009-01-21 18:20:17
klausimas speju ne i tema, Matematikos mokytojai: O kodel tada dar nebuvo diskriminanto kai jus moketes?
Paulius, 2009-01-21 18:24:39
Puikus įrašas!
Kaip tik dabar mokėmės kvadratines lygtis. Gaila, jog šis įrašas neatsirado bent para anksčiau – būčiau turėjęs galimybę apstulbinti matematikos mokytoją.
Dėl diskriminanto – o kokia ta kita formulė?
Dalius, 2009-01-21 19:06:35
Kitame įraše trumpai apie eilutes gal galėsite papasakoti? Kuo skiriasi Lorano, Teiloro ir visokios kitokios ir kas jose bendro? Koks matematinis ir koks fizikinis apibrėžimas?
Burgis, 2009-01-21 19:15:51
O, jūs mane pradžiuginote! Rytoj parašysiu viską, ką galvoju apie diskriminantą (diskriminaciją!) ir šį tą apie eilutes…
GL: neatskirčiau, žinoma, neatskirčiau, todėl ir kalbu, kad reikia žinoti vienos ir kitos kreivės apibrėžimus, o ne sakyti, mostelint ranka ore: “va, tokia kreivė…”
M, 2009-01-21 19:27:08
Nieko neišmanau pedagogikoje, bet
kam tas nuolatinis kaltės jausmo kurstymas?
Ar visi pajautę kaltę dėl savo negabumo/tinginystės pradeda stengtis?
Gerai mokosi tie, kas moka mokytis, o geras mokytojas turėtų mokyti, kaip mokytis.
Burgis, 2009-01-21 19:47:46
M.: kodėl kaltės jausmas? Pedagogika yra sritis, kurioje nuolatinis keitimasis patirtimi, naujais būdais, pateikimo formomis yra kur kas svarbesni dalykai nei, tarkime, pramonėje. Pedagogas visą laiką turi ieškoti, kaip tą ir aną pateikti trumpiau, aiškiau, suprantamiau, o kai tik randa – papasakoti kitiems. Tai ir skatinu daryti.
matematikos mokytoja, 2009-01-21 21:05:15
F.Ch. Diskriminanatas yra aukštosios matematikos (irgi labai nemėgsti šio termino, nes matematika negali būti žemoji :)) sąvoka. Tai skaičius, padedantis nustatyti polinomo (mokykloje tai kvadratinis trinaris) šaknis. Kartais taip atsitinka, kad aukštosios matematikos sąvokos, kol atkeliauja iki mokyklinės matematikos, būna iškreipiamos arba suvulgarinamos, kas ir atsitiko su diskriminantu. Mano nuomone, jis ne palengvino, o pasunkino kvadratinės lygties sprendimą. Lietuvos mokyklose jis gyvena jau 30 metų. Kaip išspręsti kvadratinę lygtį be jo? Labai paprasta, išskaidyti tiesiniais dauginamaisiais. Bet šiais laikais mokinimas šis būdas beveik neįveikiamas, nes reikia mastyti. Daug lengviau iškalti keletą formulių ir mechaniškai, būtinai tik su skaičiuokliu, kažką suskaičiuoti.
matematikos mokytoja, 2009-01-21 21:08:31
Atsiprašau. Turėjo būti: …nemėgstu ir …mokiniams.
Ronaldas, 2009-01-21 21:22:10
O iš manosios pusės būtų prašymas supažindinti liaudį (žinoma, tuo pačiu ir mane) su sigma ir binomais 🙂
GL, 2009-01-21 21:52:33
As neturejau galvoje jokio skaidymo, paprasciausiai yra formule (-b +/- sqrt(b^2-4ac))/2a ir viskas. Uztenka pasakyti, kad kai po saknimi neigiamas skaicius, realiu sprendiniu nera (kol moksleiviai nezino apie kompleksinius).
O pas mus viskas atvirksciai…
Pvz. straipsnis lietuviskoj vikipedijoj:
http://lt.wikipedia.org/wiki/Kvadratin%C4%97_lygtis
Parasyta, kas yra diskriminantas ir kaip susijes su sprendiniu skaiciumi, o ka su juo daryti – pamirsta parasyti… :]
Vietoj to prirasyti absoliuciai trivialus ir bereikalingi dalykai apie “nepilnasias lygtis”.
Palyginimui paskaitykite angliska versija 🙂
Vainius, 2009-01-22 03:09:23
Brėžinyje su direktrise truputį trūko pažymėti, kad atstumų-atkarpų kampai su direktrise sudaro statų kampą, nes vienas iš jų iš akies žiūrint truputį palinkęs, ir nevisiem aišku, kas tas atstumas iki direktrisės-tiesės.
O, GL, keista, kad per minutę-kitą pats nesugalvojot, kaip išvesti lygties sprendimo formulę, vietoj to kad atsimint ar nueit į MatLab (na, aš taip greitai tikrai nebūčiau sugebėjęs, bet žinant jus, tai būtų natūralu). 🙂
Aurelija, 2009-01-22 08:48:28
O aš jau visai ir pamiršau kas tas dikriminantas 🙂 Žodis girdėtas, bet nei kas jis toks, nei su kuo “valgomas” tikrai nepasakyčiau 🙂
Raimundas Zabarauskas, 2009-01-22 08:59:00
Gerbiamas B. Burgi, grįžtant pire parabolės ir hiperbolės – kuri yra kuri? Ir ar šie fragmentai atitinka y=a/x+b ir y=a*x^2+b*x+c?
Burgis, 2009-01-22 12:58:51
Raimundui: viršuje yra hiperbolės y=1/x fragmentas, apačioje – Jūsų aprašytos parabolės fragmentas. Aišku, iškirpau ir pasukau fragmentus taip, kad būtų panašūs.
Įdomesnis klausimas toks: kokiais įrankiais ir kokiomis matematinėmis priemonėmis iš nedidelio kreivės fragmento galima atkurti tos kreivės lygtį? Ne interpoliacinę, o tikrąją!
Raimundas Zabarauskas, 2009-01-22 13:50:38
Geras klausimas. Jei turite idelius matematinius taškus, gal ir yra prasme kalbėti apie „tikrąją kreivę“.
Fizikoje turite taškus su paklaida (fizikinio atvejo modelis: išsimatavau po dvidešimt taškų nuo Jūsų jpg), todėl nėra jokių idealių kreivių, yra tik „panašiausios“.
Parabolės atveju panašumo įvertis (sakykime, nuokrypų kvadratų suma) yra keturių nepriklausomų kintamųjų funkcija (du parametrai apibrėžia direktrisę, kiti du – židinį). Belieka juos kaitalioti tol, kol bus maksimalus sutapimas (minimali kvadratų suma)).
Jei duotumėte „užlinkusį“ parabolės gabalėlį, galima būtų (empyriškai ar analitiškai) rasti jos simetrijos ašį, tuomet liktų vienas laisvas parametras (židinio atstumas nuo direktrisės). Būtų paprasta.
Beje, gal ir hiperbolė gali būti kaip nors panašiai gudriai apibrėžiama?
Burgis, 2009-01-22 14:07:55
Raimundui: 1) Jūsų pasiūlytas metodas neblogas, bet su prielaida, kad mes žinome baigtinę (ir gana nedidelę…) aibę kreivių, iš kurių renkamės.
- Žinoma, hiperbolė apibrėžiama taip: tai kreivė, kurios kiekvieno taško atstumų iki dviejų fiksuotų taškų, vadinamų židiniais, skirtumas yra nekintantis. Pakeitę žodį “skirtumas” žodžiu “suma”, gauname elipsės apibrėžimą ir net būdą (naudojant siūlą, virvutę…) elipsei nubrėžti.
Raimundas Zabarauskas, 2009-01-22 15:17:50
Ačiū.
Beje, išspausdinęs Jūsų kreives popieriuje uždėjau jas viena ant kitos ir jos… sutapo.
Ar tikrai esate įsitikinęs, kad įmanoma atskirti kuri hiperbolė, o kuri parabolė?
imbusy, 2009-01-22 15:21:18
Man labai patiko nepaminėtas faktas apie parabolės fokusą. Satelitų skersinis pjūvis yra parabolė, nes iš kosmoso ateinantys lygiagretūs spinduliai, atsispindėję nuo parabolės, visi susikerta fokuso taške. Iškart praktinis pritaikymas ir aiškiau pasidaro, kam to fokuso reik. Beje, man visur matyta parabolės formulė yra y^2 = 4px, ne y^2 = 2px.
Burgis, 2009-01-22 15:26:17
Raimundui: taigi aš ir stengiausi, beveik pusvalandį sugaišau… 🙂 Išvada tokia: iš vieno kauliuko ir archeologai ne kažin ką pasako. Kuo mažesnis kreivės fragmentas (nors ir dirbtinai padidintas), tuo didesnės paklaidos ir mažesni šansai atskirti. Štai kodėl architektai skriestuvais piešia ovalus ir pateikia juos kaip elipses. Iš tiesų nė mažiausios elipsės atkarpėlės negalima nubrėžti skriestuvu.
Burgis, 2009-01-22 15:28:13
imbusi? Nejaugi čia tas pats imbusi?
Raimundas Zabarauskas, 2009-01-22 15:36:08
Mielas B. Burgi, sutikite, pateikėte fragmentus apie kuriuos iš principo negalima nieko pasakyti (ar parabolė, ar hiperbolė):
http://www.rzu.lt/i/db_img.php?509
Rytoj aprašysiu, kaip gavau šį vaizdą (tai bent jau įdomus IT uždavinys).
Raimundas Zabarauskas, 2009-01-22 15:50:48
Beje, įdomus (matematinis) uždavinys yra klausimas:
kuris parabolės gabalėlis panašus į hiperbolę (ir kodėl)?
Burgis, 2009-01-22 15:54:25
Raimundui: aš nemaniau, kad kas nors taip įknibs į tokį menką nieką… Juk aš nieko neverčiau atpažinti – atvirkščiai, sakiau, kad to lengvai padaryti nepavyks. Bet nemeluoju: vienas yra hiperbolės, kitas – parabolės fragmentas. Tyrinėkite toliau…
imbusy, 2009-01-22 17:13:19
Na nežinau, kurį jūs laikot tuo, bet aš tai Lukas Steiblys 🙂
GL, 2009-01-22 18:42:08
O, GL, keista, kad per minutę-kitą pats nesugalvojot, kaip išvesti lygties sprendimo formulę, vietoj to kad atsimint ar nueit į MatLab (na, aš taip greitai tikrai nebūčiau sugebėjęs, bet žinant jus, tai būtų natūralu). 🙂
Priezastis paprasta – nueiti i matlab arba internete susirasti formule neuzima nei minutes… o ir as jau ne tas, kuris kazkada laimejo Lietuvos matematikos olimpiada… 😉 Dabar tikriausiai vargiai bepasipriesinciau geriausiems… Nors nesakau, kad nesugebeciau isvesti – bet tikrai ne per minute ar dvi… O be to, ir popieriaus reiketu po ranka (tai surasti irgi uzimtu kokia minute 😉 )
matematikos mokytoja, 2009-01-22 19:27:00
GL. O, koks Jūs kuklus! Lažinuosi, kad bet kokiai kvadratinei lygčiai išskaidyti tiesiniais dauginamaisiais Jums neprireiktų nė minutės, o išspręsti pagal Vijeto teoremą nė 5 sekundžių :). Ir formulės išvedimui Jums tikrai neprireiktų tų dviejų minučių 🙂 Nereikia prisiminti, tik žinoti kelią. Manau, kad tuos kelius Jūs tikrai žinote.
GZ, 2009-01-22 19:35:20
Visada galvojau, kad visų tų “bliūdų” forma – hiperbolė. Gal dėl to, kad niekada negirdėjau apie parabolės židinį. Negi praleidom matematikos knygoj ? Gal tik pamiršau. Išraiška su židiniu ir direktrise — daug įdomesnė nei kvadratinės lygties. O kas pasuka parabolę lygtyje, tas “bx” elementas ?
GL, 2009-01-22 19:47:39
🙂 na jau ko ko, bet kuklumo manyje deja yra maziausiai… Aisku, ne visada tai blogai – kartais “assertive” asmenybes tipas padeda…
Paprasciausiai kai netenka to daryti kokius 2 metus, dalykai pasimirsta… (nezinau kodel, bet paprasciausiai nepasitaike – gal del to, kad mano darbas yra daugiausiai “computational”, o ne teoretinis, t.y. neretai tenka “fit data to polynomials”, bet velgi tai darau su MatLab, o ne spresdamas kvadratines lygtis 🙂 )
GZ, 2009-01-22 20:07:35
Suintrigavote, GL. Kokioje srityje jums tenka taikyti MatLab ? Mano sumani ir labai darbšti pusseserė baigė matematiką, o dabar turi kankintis tarp kokių tai informatikų (ir kankinti informatikus 🙂 ). Norėčiau ką nors jai parekomenduoti.
Ar leisite paprašyti atsakymo vien lietuviškais žodžiais ? Sportui. Ir kad per daug neatitrūktumėt… Dėkui.
Burgis, 2009-01-22 20:31:21
O, GL į GZ kreipiasi pagarbiai – daugiskaita… :-))). Abu jūs Gediminai, abu jūs vienas kito verti, abu jūs mūsų šalies pasididžiavimas, viltis ir ateitis. Rašau tik teisybę.
***
Lukai, kur tu dabar, ką veiki, kai sekasi? Mes kasdien kalbame per “Skype” su savo Luku (kol kas – su jo mamyte Vaiva…) Stokholme – palaima! Mūsų Lukas jau turi du dantukus!
GL, 2009-01-22 20:39:33
Na sita galiu atsakyti nesunkiai – bet kokiai duomenu analizei, modeliavimui (ypac jei yra daug skaiciavimu su matricomis).
Naudojantis MatLab galima skaiciuoti, atlikti simuliacijas, daryti ivairius grafikus ir pan. tiek tiesiogiai, tiek – jeigu reikia – parasant programa (ganetinai paprasta kalba). Pavyzdziai: pradedant nuo tokiu dalyku, kaip sio grafiko (http://icwww.epfl.ch/~luksys/mokesciai.jpg)sugeneravimas :), baigiant sudetinga statistine analize ir neuroniniu tinklu treniravimu, kuriems visiems yra paruostos standartines funkcijos…
Trukumai – per letas ir kainuoja (bet institute turime, moketi nereikia…) taigi (del greicio) neretai tenka naudotis C++.
Beje, gana naujas MatLab-o konkurentas yra Python, vienas zmogus musu laboratorijoj bando propaguoti ji kiek imanoma (netgi per daug…)
Be to, girdejau yra dar kazkoks panasus paketas, kuris turi panasias funkcijas kaip MatLab, bet nemokamas…
Raimundas Zabarauskas, 2009-01-22 22:56:48
Man visuomet smagu, kai žmogus gali įveikti kompiuterį (atlikti pieštuku ant popieriaus tai, ką įmanoma atlikti ir apsieinant be MathLab).
Nors, antra vertus, architektai jau tikriausiai seniai nepiešia jokių ovalų („o kas tas skriestuvas?“)…
Vainius, 2009-01-22 23:50:38
GL, o Mathematica netenka naudotis? Mus kažkodėl universitete daugiausia jos moko, o ne MatLab’o, ir kol kas man tai visai patinka, tik įdomu ar čia tik pas mus jinai laikoma perspektyvia.
GL, 2009-01-23 00:18:43
Nezinau, man Mathematica neteko naudoti, bet kiek girdejau, sis paketas daugiausiai naudojamas butent analitinei matematikai (t.y. ivairiu lygciu sprendimui)
Pagooglinus, butent taip ir atrodo…
“Mathematica and Matlab are very different products. Mathematica focuses on quality symbolic computation and features like unlimited precision arithmetic. Matlab focuses on high speed algorithms for numerical computation.”
“I find that most research groups choose matlab for numerical solutions/simulations and mathematica for analytical solutions.”
Qt, 2009-01-24 16:59:41
Python yra puiki programavimo kalba. Atsimenu kaip kankinausi, kai teko su matlab’u rašyti programą uždaviniui spręsti. O dabar yra puiki pythono biblioteka NumPy. Pažiūrėkit http://numpy.scipy.org/ tikrai patogu ir beto nemokama bei legalu.
GL, 2009-01-24 22:47:17
Atsimenu kaip kankinausi, kai teko su matlab’u rašyti programą uždaviniui spręsti.
Idomu, koks ten uzdavinys buvo, kad su MatLab’u reikejo “kankintis” :). Python gal ir neblogas, bet jis labai skiriasi (ne vien sintakse, o ir pacia esme) tiek nuo C++, tiek nuo MatLab, ir todel man bent iki siol kazkaip nesimato tikslo ji mokytis…
qq, 2010-04-03 03:21:45
o kaip gali 1 x reiksme atitikti 2 y reiksmes?