Skaičiai yra įdomūs ne vien matematikui, bet ir kiekvienam mąstyti mėgstančiam žmogui. Pažiūrėkite, kokie minčių viražai…



Tęsinys – kitą dieną….
Atsakymai
Klausimai…, 2009-01-24 00:15:21
Man nepatinka susitarimai … Man patinka, kai visa, kas yra matematikoje, liejasi laisvai ir natūraliai. Nejaugi kompleksiniai skaičiai buvo sugalvoti tik tam, kad būtų galima užrašyti formalius kvandratinės lygties sprendinius?
Be to, kokie yra dabartiniai sveikųjų ir iracionaliųjų skaičių apibrėžimai? Kol kas mano kolekcijoje yra tik:
*natūralieji skaičiai – skaičiai, kuriais skaičiuojame daiktus;
*racionalusis skaičius – skaičius, kurį galima išreikšti sveikojo ir natūraliojo skaičių santykiu;
*realieji skaičiai – visų atkarpų ilgių aibės elementai.
Pasinaudodami savo įžvalgomis, padėkite užbaigti:
*sveikasis skaičius
*<strong)iracionalusis skaičius
…
Irid, 2009-01-24 01:12:28
Pirma žaidimo taisyklė: egzistuoja natūralieji skaičiai (1 obuolys, 2 obuoliai, …). Antra žaidimo taisyklė: tuos skaičius galima sudėti (aš turiu du obuolius, tu turi tris, mes turim 2+3=5).
Bet tai palauk, jei galima sudėti, tai turi būti ir atvirkštinis veiksmas – atimtis: jei mes turim penkis obuolius, o tu turi tris, tai aš turiu 5-3=2. Bet jei mes turim tris, o tu turi penkis, tai aš turiu 3-5=??? Aš matyt du obuolius skolingas. Norėdami išgelbėti atimties veiksmą, kad jis turėtų prasmę ir tokiu atveju, mes papildomai susigalvojam neigiamus skaičius ir nulį. Dabar šiuos naujus sveikuosius skaičius galima sudėti ir atimti neribotais kiekiais, ir taip darydami mes neišeinam iš sveikųjų skaičių ribų. Kitaip sakant, turim tobulai išbaigtą skaičiavimo sistemą.
Kai atsibosta sudėtis (3+3+3+3+…), mes ją sutrumpintai užrašome kaip daugybą (3*5=15). Bet tada turi būti ir dalyba (15/5=3)? Tačiau pvz. 5/3 nėra joks mums žinomas skaičius, todėl mes prikuriam daugiau skaičių (racionaliųjų), kad išgelbėtume dalybą.
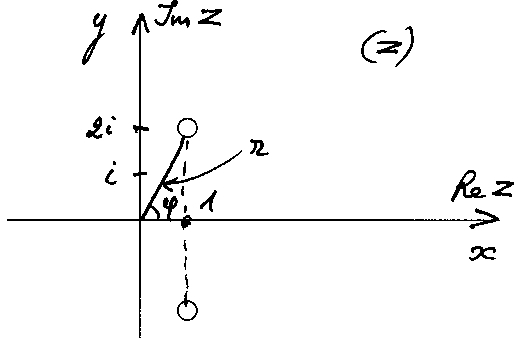
Kai atsibosta ir daugyba (4*4*4*4*…), mes ją sutrumpintai užrašome kaip kėlimą laipsniu (4^6=2048). Bet tada turi būti ir šaknis (sqrt[6](2048)=4)? Tačiau, nelabai sunku įrodyti, kad pvz. sqrt(2) nėra joks mums žinomas skaičius, todėl prikuriam daugiau skaičių (iracionaliųjų), kad išgelbėtume šaknį. Bet to negana, nes sqrt(-1) irgi nėra joks skaičius, todėl prikuriam dar daugiau skaičių (kompleksinių).
Gobšumas ir tingumas mūsų neapleidžia, ir mes dirbame ne su vienu skaičiumi, bet su jų rinkiniais – su vektoriais. Juos galima sudėti, atimti, dauginti. Bet jei padalini vieną vektorių iš kito, ką gauni? Naują objektą – tenzorių. Tenzorius išgelbėja vektorių dalybą!
Deja Vu? Viskas tas pats per tą patį. Plačiau žiūrint, kompleksiniai skaičiai niekuom ne labiau komplikuoti už pvz. neigiamus. Tiesiog toks klaidinantis pavadinimas, atseit kompleksiniai. Gal sunkumas tik tame, kad įmanoma įsivaizduoti 5/3 obuolio, bet 2+6i jau sunkiai… Užtat kai gaunate per nagus nuo elektros u=u_0exp(-iwt), visas kompleksiškumas labai aiškiai pasijaučia 🙂
Raimundas Zabarauskas, 2009-01-24 05:45:50
Bravo, Irid!
O ar tenzorius galima sudauginti?
Burgis, 2009-01-24 08:20:35
Ačiū, Irid, Tu man labai padėjai! Kiti turi žinoti, kad Irid (Airidas) – įvairiausių, neįtikėčiausių konkursų ir olimpiadų laureatas – tiesiai po KTUG išvažiavo studijuoti į Milaną. Neabejoju, kad italai pajuto, kas yra kas moksle…