Korepetitorius dirba chaotiškai – taip, kaip gyvenimas pateikia mums iššūkius. Nebaigęs kalbos apie kompleksinius skaičius ir funkcijas (žadu baigti…), pateikiu elementariausią aiškinimą apie sinusų reikšmes.

Pradėkime. Įsivaizduokite statųjį trikampį. Įsivaizduojate? Nebraižysiu. Statinio prieš kampą ilgio santykis su įžambinės ilgiu yra to kampo sinusas. O dabar įsivaizduokite, kad tos įžambinės ilgis yra vienetas (Koks vienetas? Na, jei turite vietos, tai vienas metras, jei vietos mažiau – viena pėda, vienas decimetras, vienas colis, vienas centimetras. Supratote? Vienas – sutartinis ilgis.) Kas dabar yra sinusas? Žinoma, statinio prieš kampą ilgis! Taigi sinusą galima išmatuoti (nemamirškite įvertinti, koks yra sutartinio vieneto ilgis), pamatyti, paliesti, net palaižyti… Tai kam mokytis kažkokias lenteles?!
O dabar įsivaizduokime tą trikampį vienetiniame apskritime (apskritime, kurio spindulys yra sutartinio vieneto ilgio). Pirmajame ketvirtyje nubrėžkime tris populiariausius kampus: 30, 45 ir 60 laipsnių dydžio. Vertikalūs statiniai yra tų kampų sinusai, matote? Sunumeruokime sinusus nuo mažiausio iki didžiausio. Ar sutinkate su paveikslėlyje pateikta numeracija? Jei nesutinkate, okulistai jums padės…
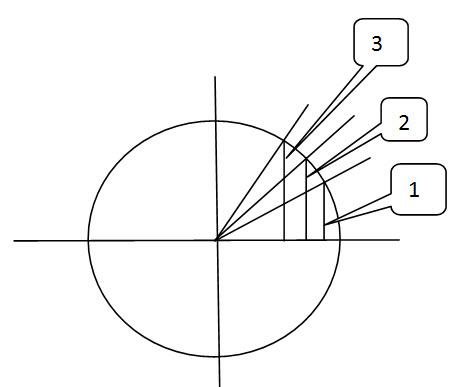
Dabar įsivaizduokite, kad kažkoks pokštininkas visus numerius (ilgius) padalijo iš 2. Ar pasikeitė numeracijos tvarka? Ne.
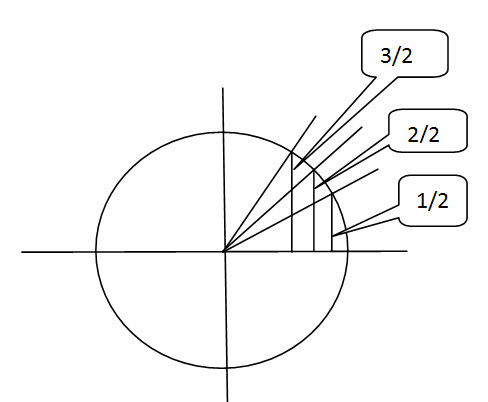
Leiskime dar tam pokštininkui „uždėti“ po kvadratinę šaknį ant kiekvieno skaitiklio – numeracijos tvarka vis tiek nepasikeis. O jūs matote 30, 45 ir 60 laipsnių kampų sinusų reikšmes! Visam gyvenimui…
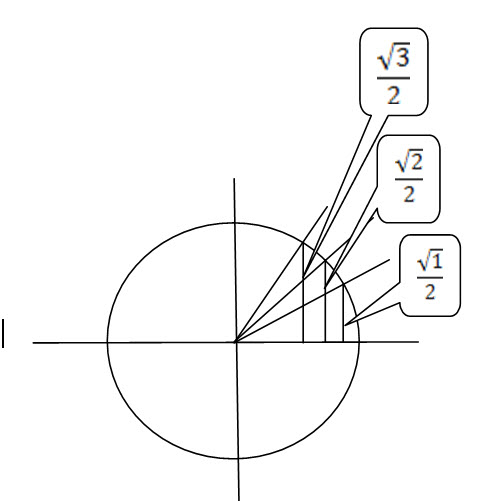
Pridurkime, kad reikia „lakios“ vaizduotės nematyti, kad sinusas nulio (laipsnių arba radianų) yra nulis (nėra jokio vertikalaus brūkšnelio), o sinusas stačiojo kampo yra vienetas (statinis lygus spindulio ilgiui).
Tame „magiškame“ apskritime matote (matote, o ne išmokstate!) viską: periodiškumą, ženklus, redukciją ir kt. Ačiū, kad patikėjote.
Atsakymai
EtikMat, 2009-01-24 15:48:52
“matote (matote, o ne išmokstate!)” matyti !=(nelygu) suprasti
Qt, 2009-01-24 16:24:40
Nors jau seniai baigiau mokyklą, bet tokio puikaus paaiškinimo negirdėjau. Dėkui.
matematikas, 2009-01-24 18:13:29
Naudojant tokias istorijas galima turbut matematikos vadovelius mokleiviams gerokai patrumpinti. Arba jei tokias istorijas zinai, tiesiog is viso iprastu vadoveliu nenaudoti 🙂
vyr, 2009-01-25 16:30:46
Sinusas – taip, su jais būna problemų. Kosinusas? Atleiskit, bet nėra tokio organo…
Burgis, 2009-01-25 17:08:19
Sinusas stovi, kosinusas – guli…
qq, 2010-04-03 03:39:56
man tai biski kitaip sake 😀
pasiemi kumsti 😀
ir skaiciuoji issikisusius kaulelius
1 kaulas 30, 2 kaulas 45, 3 kaulas – 60
o sakni ir dalyba is 2 tik prirasyti 🙂
nors ir 0 (0/2=0)ir 90((sqrt(4)/2)=1) gerai iseina 😀
Pwl, 2014-07-09 15:55:00
Dar besimokydamas mokykloj kartą nuėjau pamokyt jaunesnę kaimynę trigonometrijos. Ji daug žinojo,bet ne viską suprato. Problema buvo ta, kad viską turėjo išmokt mintinai – formules , reikšmes. Panaši terapija su apskritimu padėjo. Nors su fiziką jai buvo panašiai. Sakau, “yra viena formulė ‘ F=ma’…” Ji mane pertraukia : “…o pala tai masės ir pagreičio formulės yra, reikia išmokti…” Ne, sakau, yra F=ma, o kitas turi mokėt išsivest. Padėjo 😉