Šios svetainės temoje „Dar vienas įrodymas“ (rugpjūčio 6 d.) buvo toks Mato komentaras:
*
O man dar patiko lengvas tikimybių uždavinukas: 0,8 tikimybė, kad turi savo namų raktą, o jei turi, tai 0,5, kad vienoje kišenėje, ir tiek pat kitoje. Pasitikrinini vieną kišenę – rakto nėra. Kokia tikimybė, kad jis kitoje kišenėje?
*
Aš nežinojau, kuris čia Matas, paprašiau po savaitės paskelbti sprendimą.
Vakar gavau štai tokį laišką:
*
Labas vakaras.
Rašau Jums iš Rusijos, matematikos stovyklos. Čia interneto nėra (draugas dabar mobiliuoju leido pasinaudoti), todėl neatrašiau jums, kai prašėte pateikti uždavinio sprendimą – atsiprašau dėl to. Jis trumpas ir paprastas. Tikimybės tokios: 0,4, kad raktas kairėje kišenėje, 0,4, kad dešinėje, ir 0,2, kad rakto neturime. Patikrinus vieną kišenę, liko tik du variantai, o jų santykis – 1:2, todėl atsakymas yra 2/3.
Pagarbiai,
Matas Grigaliūnas
***
Taigi čia mūsų matematikas Matas! Dabar jūs suprantate, kad ne tik matematika yra gėris, grožis, precizika, bet ir ją išmanantys žmonės yra tokie.
*
Buvau pažadėjęs paskelbti šiek tiek panašų į Mato pateiktąjį uždavinį, tai ir skelbiu. Jį esu įrašęs į konspektą savo studentams…
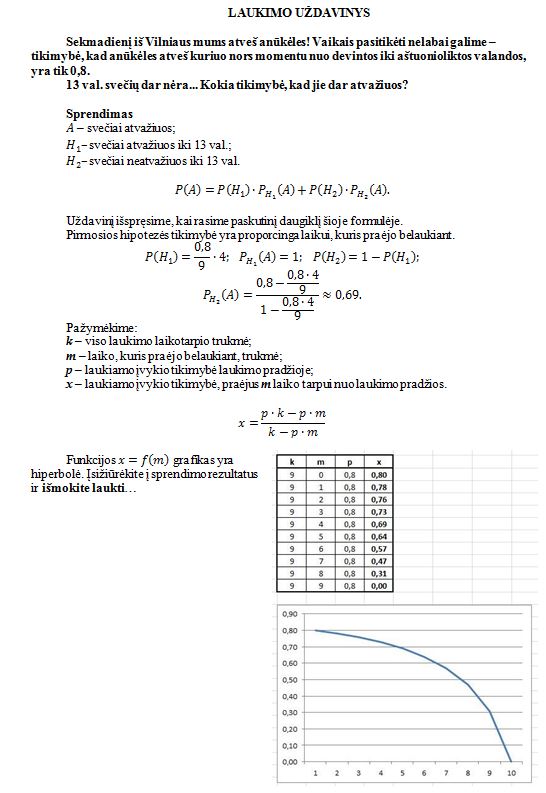
Atsakymai
Burgis, 2013-08-20 08:38:24
Man taip patinka…
Grigalius, 2013-08-20 16:21:24
“Pirmosios hipotezes tikimybe yra proporcinga laikui…” – argi nera cia pasleptos prelaidos, kad atvaziavimo tikimybes pasiskirstymas yra uniforminis? Juk galetu buti normalus 🙂
Jurgis, 2013-08-20 16:26:38
hm, o kodėl netiktų logika, kad jei nėra vienoje kišenėje, tai rasti kitoje tikimybė patampa – 0.8 (nes papildoma informacija pakeičia tikimybių pasiskirstymą)?
Man ūkiškai atrodo – analogiškai kaip metama moneta gali atsiversti – 0.5 herbas arba 0.5 skaičius. Jei sužinom, kad neatsivertė herbas, tai garantuojam 100%, kad atsivertė skaičius (nebent ore pakibo :P).
Jurgis, 2013-08-20 16:28:44
nes buvo įvardinta fiksuota tikimybė 0.8, kad tu turi savo namų raktą…
petras, 2013-08-20 17:09:30
man atrodo Jurgis teisingai sako
Random, 2013-08-20 17:25:44
Tai tikimybės ir pasikeičia. Viena tampa 0,(3), o kita tampa 0,(6).
Burgis, 2013-08-20 19:36:56
Aha, „užsikabinote“! Šaunuoliai!
Kol kas atsakau Grigaliui: taip, labai teisingai pastebėjai – čia suprantama, kad yra vienodai pasiskirsčiusi tikimybė (stačiakampis skirstinys). Žinodamas savo vaikų įpročius teigiu, kad šis skirstinys geriau tinka nei normalusis, bet iš tiesų netinka nei vienas, nei kitas…
jurgis, 2013-08-20 22:56:48
pasvarsčiau bevaikščiodams, atrodo ūkiška logika tinka tik primityviam atvejui – su 2 variantais.
Bendras dėsningumas visgi – likusių tikimybių suma proporcingai persiskaičiuoja į 100% – ir Mato sprendimas tada ok, ir monetos atspėjimas ok.
Man padėjo įsivaizdavimas tokio eksperimento:
turim 100 sunumeruotų popierukų. Juos sumaišom ir atsitiktinai padalinam: 20% į šoną, 80% sau (ir įsidedam į vieną iš 2 kišenių – 40 ir 40).
Tada tarkim, kad ieškom lapuko su numeriu X. Vieną iš kišenių iškraustom ir nerandam… Kokia tikimybė, kad jis kitoje kišenėje? 🙂
Burgis, 2013-08-21 08:38:06
Matematikai, prašyčiau pateikti Mato uždavinio formalų sprendimą, studentams pateikiamų formulių bazėje! Galite šiek tiek nusirašinėti nuo manojo uždavinio…
Kristupas, 2013-08-22 22:42:19
Taigi uztrukau bet vis delto vokietis laiko zuvytes ar ne taip Direktoriau?
Burgis, 2013-08-23 08:42:31
Kristupui: taip, vokietis laiko žuvytes.