Puikus šios svetainės lankytojo (lankytojos?) „C.“ komentaras
„Iš Nobelio premijos laureato Richard Feynman puikios knygos Surely You’re Joking Mr. Feynman:“ ankstesnėje matematikos temoje verčia mane tęsti temą apie mano naująją funkciją…
*
„Krepšiasvydis“ neprigijo, „vaizduoklis“ neprigijo, o „išmanusis“ (telefonas, spausdintuvas) prigijo. Tiesa, mano pasiūlytasis terminas „išmoningasis spausdintuvas“ (smart printer) virto terminu „išmanusis spausdintuvas“. Galėčiau ginčytis…
Iš lotyniškojo imaginarius labai gerai prigijo i: i*i=-1.
Iš graikiškosios „sigma“ raidės labai gerai prigijo sumos ženklas.
Ir integralo ženklas prigijo…
Ir gama funkcija kaip faktorialo apibendrinimas man patinka…
Taigi bandysiu jus pripratinti ir prie savo naujosios funkcijos! Ji labai įdomi, tikrai!

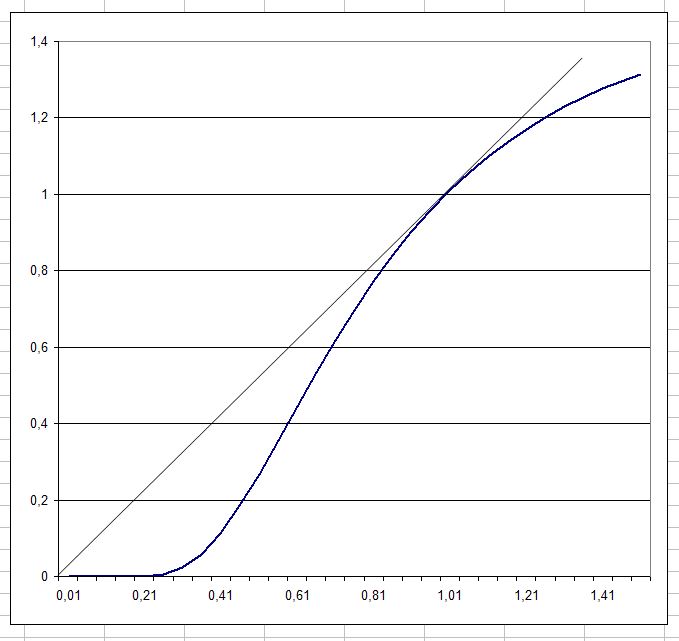

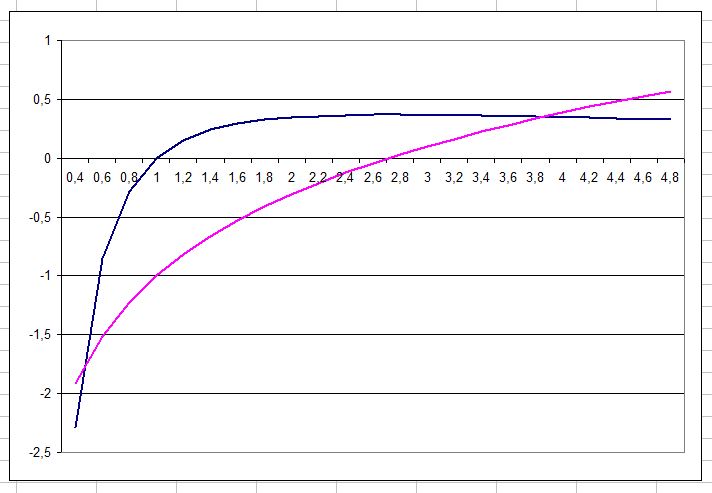
Patikslinti galima „Excel“ programa: apytiksliai 0,45 ir 3,85.
***
Gera turėti laiko tokiems žaidimams!
Atsakymai
Burgis, 2015-03-12 10:11:49
Jūs gerai balsavote už matematiką! Dar kartą, prašau…
Sokolovas, 2015-03-12 10:49:23
Gerb. Burgiui
Dėkui.
Niekad neneigiau grafikų vaidmens, TIRIANT lygtis ( nelygybes, lygčių sistemas, lygtis bei nelygybes su parametru…).
Tačiau tai, ką Jūs parodėte, vis dėlto yra lygties tyrimas, o ne sprendimas.
Matematiškai argumentuosiu taip: Lygties TYRIMAS parodė, kad yra tik du sprendiniai. Po to, tęsiant tyrimą, galima rasti sprendinių izoliacijos intervalus ( nurodytu, o ne “atmetus nepatikusius skaitmenis”, tikslumu).
Ir dar. Grynai žmogiškai SPRENDIMĄ suvokiu kaip žmogaus, apsiginklavusiu rašikliu ( ar kreida), darbą. Neduok Dieve man sulaukti laikų, kai uždavinių sprendimo grožį nusavins kažkokie “ekseliai”…
Esu konservatyvus? Aš šito ir neneigiu! 🙂
Burgis, 2015-03-12 10:56:20
Sokolovui: ne, aš su Jumis nediskutuosiu, nebijokite… Tik mane kankina smalsumas: kas Jūs? Kiek Jums metų? Kur Jūs dirbate, dirbote? Kokių matematikos darbų esate pateikęs visuomenei?
*
Kadaise mano katedroje dirbo vienas Sokolovas, bet aš taip su juo arčiau ir nesusipažinau…
*
Tai, žinoma, nebūtina, bet jei Jūs spragtelsite voko ženklelį šios svetainės tituliniame puslapyje ir parašysite man keletą atsakymų, tai aš geriau žinosiu, ką su Jumis daryti… 🙂
Sokolovas, 2015-03-12 13:31:07
Gerb. Burgiui
Neatsidaro man tas “vokelis”…
KPI Bendrosios matematikos katedroje ( vedėjas buvo A. Andriuškevičius) dirbau iki 1991-jų metų. Po to atleistas pagal etatų mažinimą ( neturiu mokslinio laipsnio). Dėsčiau tuometiniame lengvosios pramonės fakultete, taip pat ruošdavau studentus olimpiadoms, kurių tais laikais būdavo…( buvo įdomu rungtis su kitos katedros ruoštais “skaičiavimo technikos fakulteto” studentais).
Po to dirbau ( bei tebedirbu) suaugusiųjų mokymo centre , turiu mokytojo-eksperto laipsnį.
Parašiau kelias knygutes, tarp jų-“Lygtys su parametru” ( Jūs ją turite), matematikos vadovėlį suaugusiems ( 7-10, 11-12), ir keletą kitų …
Man 53 metai, tad esu “išeinančios kartos” atstovas..:)
Esu konservatyvus, bet ne dogmatikas. Stengiuosi savo nuostatas grįsti dėsniais, o ne “autoritetais”..
Burgis, 2015-03-12 13:49:16
Sokolovui: ačiū! Aš galėjau ir atspėti, kad Jūs tas pats Sokolovas, kuris parašė knygas su Toma Giedraitiene-Lileikiene…
Daugiau – jokių komentarų apie Jus. Prisiminkite mano nurodytus apribojimus.
Random, 2015-03-12 14:54:52
Na, kai x= 1/2 ar koks kitas panašiai gražus skaičius – taip pat nesunku mintinai suskaičiuoti ar atspėti sprendinį.
O šiaip, ar įmanoma gan sudėtingai funkcijai patikrinti/įrodyti, kad grafikas nebeužsilenkia kur nors toli toli nelendant į diferencialą? Arba iš kitos pusės: kaip nuspręsti kiek pasipaišyti grafiko, kad matytum visus svarbiausius taškus?
Burgis, 2015-03-12 15:16:43
Random: aš paprastai darau taip: „Excel“ programa pabandau grubiai, „dideliais žingsniais“, o paskui patikslinu.
Žinoma, funkcijos monotoniškumo intervalams rasti geriausiai tinka išvestinė, bet dažniausiai turi būti „kažkas tokio“, kad funkcija pakeistų monotoniškumą. Tą „kažką tokio“ galima pamatyti arba bent įtarti…
skaitytojas, 2015-03-12 15:46:27
Gerb. Sokolovui-apie kokią išeinančią kartą kalbate,jei Jums 53 ? Dabartiniam Italijos prezidentui Mattarella yra 73 metai (ankstesniajam Napolitano buvo 89 metai).
Sokolovas, 2015-03-13 11:04:05
NETIKĖTAI APSIREIŠKĖ
Išspręskite be “ekselių” bei kitokių “naujovių”:
sin(sinx+x – 0.5) + sinx = 1
Burgis, 2015-03-13 11:24:25
Sokolovui: x=pi/6.
Sokolovas, 2015-03-13 11:42:40
Gerb. Burgiui
Lygtis yra ekvivalenti lygčiai
sinx=0,5
Todėl sprendinių aibė: pi/6 + 2pi k bei 5pi/6 + 2pi k
Burgis, 2015-03-13 12:04:48
Sokolovui: aš parašiau atsakymą, vos pažiūrėjęs į lygtį, o Jūs parašėte atsakymą, bet neparašėte sprendimo. Neparašėte metodo! Ai, ai, ai, kaip negerai!…
Sokolovas, 2015-03-13 12:32:24
Gerb. Burgiui
PATEIKIU SPRENDIMĄ:
Keitiniu y=sinx + x – 0,5 lygtį keičiame sistema, kurios pirmoji lygtis
siny + y – x = 0,5, antroji lygtis:
sinx + x – y = 0,5.
Iš čia gauname:
(siny + y) – ( sinx + x) = x – y.
Kadangi funkcija f(t)=sint + t yra didėjanti visoje realiųjų skaičių aibėje ( nes išvestinė cost + 1 nėra neigiama, o nuliui lygi tik pavieniuose taškuose), tai pastaroji lygybė
f(y) – f(x) = x -y yra teisinga tada ir tik tada, kai
y = x.
Taigi, sinx + x – 0.5 = x, t.y. sinx=0,5.
Metodas: Kintamojo keitimas, bei funkcijos monotoniškumo taikymas.
IŠTAKOS: Galima sukurt daugybę tokių lygčių, remiantis analogiškai įrodomu bendresniu teiginiu:
Teorema: Jei funkcija f(x) yra didėjanti visoje R, tai lygtys f(x) =x ir f(f(x)) = x yra ekvivalenčios.
Beje, čia nagrinėta lygtis gimsta iš minėtos teoremos ( tik spręsdamas jos nenaudojau, bet kilmės tai nepaneigia…), imant
f(x) = sinx + x – 0.5.
Burgis, 2015-03-13 12:37:13
Sokolovui: va, dabar gerai! Bet galima paprasčiau…
Sokolovas, 2015-03-13 12:42:22
Gerb. Burgiui
Taip, metodai vienatvės nemėgsta 🙂
Galima ir Lagranžo teorema pasinaudot lygties
siny- sinx = 2(x-y) tyrimui…
Gal ir kitaip galima…
Paulius, 2015-03-25 23:25:37
Visada smagu pasibandyt ant http://graph.tk