Pažiūrėkite, studentai, pažiūrėkite, kokį žavingą dalykėlį aš jums parengiau!
O štai ir darbo laukas: monte
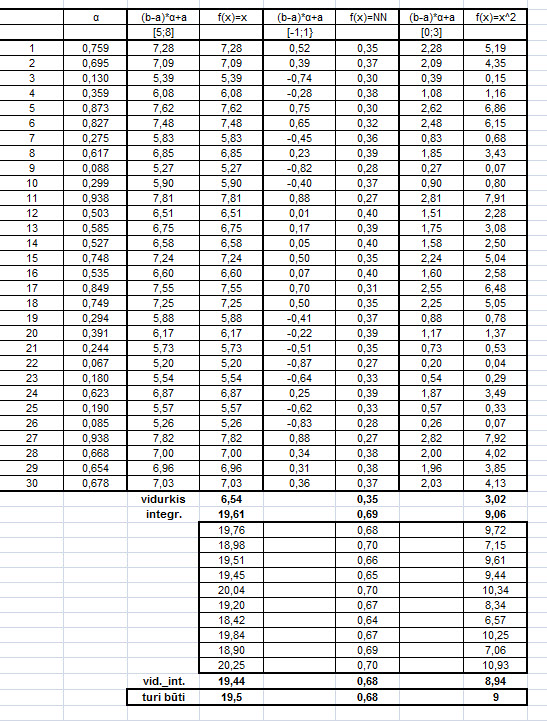
Ką čia matote? Matote, kaip “Exel” programa sugeneruoja trisdešimt atsitiktinių dydžių, vienodai pasiskirsčiusių intervale [0;1]. Kitame stulpelyje mes išplečiame intervalą iki pageidaujamo (atkreipkite dėmesį į formulę). Tai padarėme tris kartus, vis pasirinkdami kitokį intervalą – tokį, kuriame duotas integralas (tokį, kokie yra integralo rėžiai). Ką integravome? Iš pradžių – labai paprastą funkciją f(x)=x, kad galėtume mintinai apskaičiuoti rezultatą ir pasitikrinti, ar viskas gerai su Monte Karlo metodo lauku. Po to apskaičiavome “vienos sigma” taisyklės rezultatą. Kaip įdomu! Pagaliau apskaičiavome plotą po “mokykline” parabole.
Prisimenate, “Exel” funkcija RAND turi įdomią savybę: jis kaskart iš naujo pateikia kitą rinkinį, vos tik ką nors pakeičiame lape. Tuo pasinaudodami bematant visus tris integralus apskaičiavome ne vieną, o dešimtį (vienuoliktas tas, kuris nuotat kinta…) kartų. Tada pateikėme rezultatų vidurkį, kuris puikiai dera su tikrosiomis reikšmėmis. Bet pastebėkite, kad išsibarstymai nemaži, ypač trečiuoju atveju, todėl trisdešimties atsitiktinių “šūvių” į integravimo intervalą – mažoka. Trijų šimtų – visiškai pakanka.
Viską išstudijuokite, viską išbandykite – jums patiks!
Atsakymai
Vainius, 2009-05-02 20:03:06
Super!
Tik galėjot dar parašyt, kaip iš funkcijos reiškmių vidurkio gaunat integralo reiškmes, kad padauginat iš intervalo pločio (nes turint vidutinį aukštį virš x-sų ašies, kad rasti plotą, t.y. integralą, reikia padaugint iš pločio). Tiesiog dėl aiškumo 🙂
Vainius, 2009-05-02 20:32:46
O gal galėtumėte pakomentuoti, kuo šis metodas pranašesnis už tradicinį integralų skaičiavimą? Tiesa, būna integralų, kurių šiaip neapskaičiuosi, bet apytiskliai dažnai juos galima suskaičiuot išskleidžiant Teiloro-Makloreno eilute, arba tiesiog duodant kompiuteriui dalint į stulpelius ir sumuot…
Burgis, 2009-05-02 20:38:25
Vainiui: ačiū! Manau, kad šis Monte Karlo metodo pritaikymas yra tik studentams, tik iliustracija – lengviausiai suprantama. Nemanau, kad kas nors šiais laikais taip integruotų… Bet metodo idėja man labai patinka!
Jovita, 2009-05-06 18:25:41
Direktoriau, – as naudojau Monte Carlo darbe… Skaiciuojame investiciju verte – “random” vyriausybes sprendimai, infliacija, populiacijos sveikata, moksliniai atradimai, konkurencija ir t.t. O svarbiausia modeliai parodo ne tik $ investicijos atsipirkimu pasiskirstyma, bet kokie faktoriai tures didziausia reiksme (decission tree).
Hahaha – kai pirma karta sukuriau Excelyje modeli naudojant “rand”, tai mano vargsas kompiuteris skaiciavo visa savaitgali, kol galiausiai pirmadienio ryte turejom atsakyma:) Dabar isigijom @risk programa – zymiai greitesne:) Ir klientai siuos modelius naudoja. Tikiuosi ir daugelis Jusu studentai juos naudos praktikoje. Sekmes!
petras, 2009-05-08 11:37:22
Ne į temą: kažkada nesenai, man rods JAV studentai norėjo rast didžiausią pirminį skaičių, tai laikė kompą įjungtą beveik metus man rods (visą tą laiką skaičiavo jis :DD) (celeroną 800tinį artai 600). iki
rudis, 2009-08-29 22:16:05
nezinau , kokia sio blogo politika del nuorosu ,bet surizikuosiu .. Trumpai bet idomiai galit pasiskaityti siek tiek apie Monte Carlo metoda adresu :
http://www.itpa.lt/mathematica/24Monte_Carlo.html
Vardenis Pavardenis, 2009-09-22 23:54:47
Turetu buti rukomas jei MONTE KARLO 😀
O.S., 2010-12-11 22:56:48
Gerb. Dėstytojau gal galėtumėt pakomentuoti „vienos sigmos“ taisyklę?