Turėdamas laiko priminsiu savo studentams, moksleiviams ir švietimo vadovams, funkcionieriams (pavyzdžiui, parengusiems 242 psl. ataskaitą…) vieną matematinį principą: kartais trumpiau, aiškiau ir naudingiau paneigti, negu teigti. O kartais tiesiog būtina paneigti, kad nebūtų klystama. Štai puikus pavyzdys iš interneto (suraskite adresą ir pažiūrėkite dinaminį vaizdelį!):
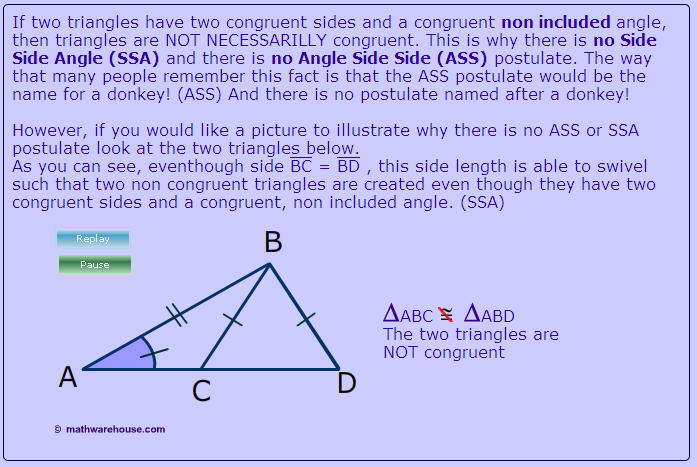
Būtinai perskaitykite tekstą – aš labai mėgstu tokias asociacijas (ASS), padedančias prisiminti… :-).
*
Čia tiks ir apibendrintas geometrijos principas: jei pagal duotus duomenis galima sukonstruoti vienintelį geometrinį objektą, tai visada pagal tuos duomenis galima rasti visus kitus to objekto parametrus: kampus, ilgius, plotus, tūrius. Tai labai įdomu! Žinodamas, kad galima rasti, jaunesnių klasių moksleivis smalsauja – kaip rasti? Kartais tenka jam pasakyti – palauk pirmo kurso universitete…
***
Liepkite man pritaikyti šį principą! Laukiu duomenų.
Atsakymai
Smokas, 2010-08-16 17:37:35
kad jau niekas daugiau nesiryžta, tai tiek to.
Liepiu Jums pritaikyti šį principą.
O duomenų kokių konkrečiai reikia ? 🙂
Burgis, 2010-08-16 20:01:03
Smokui: ne, ne taip… Jūs, pavyzdžiui, man sakote: sferos paviršiaus plotas -200 kv. cm. Raskite ta sfera apgaubto rutulio tūrį. Ir aš rasčiau! Bet įdomiau su trikampiais, daugiakampiais…
Ir nebijokite manęs…
Smokas, 2010-08-17 09:37:14
Kažin ko nesugalvoju. Gal tai tiks ? Yra trimatė sistema XYZ. Min reikšmė 0, max reikšmė 1. Pirmo trikampio viršūnių koordinatės:
X(0,6097;0,3111; 0,0195)
Y(0,2053;0,6257;0,0609)
Z(0,1492;0,0632;0,7446)
Antro:
X(0,4625;0,2428;0,0112)
Y(0,3563;0,6749;0,0709)
Z(0,1455;0,0823;0,7429)
Kokio skersmens sfera telpa į abu trimačius trikampius ir kokios jos centro koordinatės ?
Smokas, 2010-08-17 10:30:33
tarp kitko paaiškinsiu iš kur ištraukiau šituos skaičius.
Pirmo trikampio koordinatės tai AdobeRGB spalvų profilio RGB kolorantų tristimulai. Antro trikampio mano monitoriaus spalvų profilio RGB kolorantų tristimulai.
Burgis, 2010-08-17 11:31:16
Smokui ir kitiems: tai fantastiška ir simptomatiška! Žmogus moka ir žino tiek daug, kad suprantamai nieko pasakyti nebegali… Kuo ilgiau gyvenu, tuo daugiau sutinku Smoko tipo žmonių.
*
Kas yra trimatis trikampis (šiuo atveju; čia yra du trikampiai trimatėje erdvėje; o į ką turi tilpti sfera?)? Ką reiškia „sfera telpa į abu trimačius trikampius“? (už šią frazę turėtų skirti Nobelio literatūros premiją…) Aš koordinačių plokštumos yra ribojančios plokštumos?
Trumpiau – nieko nesupratau… Ir čia labai svarbi pastaba: jūs niekada nesiimkite spręsti uždavinio, jei sąlyga yra nors šiek tiek neaiški! Nes negalima pagauti juodos katės tamsiame kambaryje, jei jos ten nėra.
Smokas, 2010-08-17 12:27:07
atsiprašau labai už netiklumus. Nepervertinkite mano žinių. 🙂
Trimačiu trikampiu šiuo atveju aš pavadinau trikampę piramidę. Abi jos persidengia viena su kita. Kokio dydžio sferą galima patalpinti į jų bendrą plotą. Paaškinimas gal ir nematematiškas, bet gal suprantamesnis ? Koordinačių ploštumos yra ribojančios.
Burgis, 2010-08-17 12:31:48
Ačiū, Smokai, dabar galvosiu, ką supratau… Vienas atsakymas jau aiškus – pagal tą principą, kurį minėjau, tai vienareikšmis uždavinys, todėl jį galima išspręsti. Bėda, kad aš nemoku braižyti trimatėje erdvėje…
Tomas, 2010-08-17 12:31:58
Iš dviejų trikampių nelabai išeis gauti piramidę, galbūt turite omenyje prizmę, kurios pagrindai yra trikampiai?
O jeigu visgi turite omenyje piramides, tai gal reikėjo nurodyti, kad jūsų duotų koordinačių trikampiai yra tų piramidžių pagrindai, o abiejų viršūnės kad ir koordinačių sistemos pradžia 🙂
petras, 2010-08-17 14:09:33
ai, dar papildymas klausimui. šiaip čia manau turėtų būt, kokio didžiausio skersmens sfera telpa, nes paėmus labai mažą, tikrai tilps ir tokių gali būt visa begalė. o šiaip pora integralų priartėjimo principu ir uždavinys išspręstas :DD
petras, 2010-08-17 14:12:16
ir dar tiesa, kompiuterio pagalbos gal prireiktų, bo mintinai ar ant popieriaus spręst tokius uždavinukus turbūt laiko daug atima ?
Smokas, 2010-08-17 14:20:05
čia įdomus straipsniukas apie tai kaip įvairių tipų ir specialybių žmonės turi savo specifinę kalbą:
http://qualityinprint.blogspot.com/2010/08/techtalk.html
Burgis, 2010-08-17 15:13:03
Na va, Tomas jau paklausė. Ir aš vėl turiu klausti: Smokai, kur turi būti ta sfera? Koks ryšys kiekvieno trikampio su koordinatinėmis plokštumomis? Supraskite gi, kad reikia paaiškinti: štai vienas taškas erdvėje; jis (tikriausiai) jungiamas su kitu tašku erdvėje, o šis – su trečiuoju tašku. Na, ir kas? Gavome „kybantį“ trikampį. Kur tas erdvinis kūnas? Plokščias trikampis erdvėje nėra kūnas!
Kol kas Jūsų, Smokai, kalba labai panaši į tą, kuri pateikta nuorodoje…
Aurelija, 2010-08-17 15:14:11
netikėtai gavau į el. paštą šitą filmuką 🙂 buvo juoko visai dienai 🙂
http://www.youtube.com/watch?v=jBNw7-T3G2w&feature=related
Smokas, 2010-08-17 15:29:54
bet juk as pateikiau kiekvieno tasko po tris koordinates. Juos sujungus tarpusavyje gauname piramide. Kur cia plokscias trikampis ?
Smokas, 2010-08-17 15:38:35
… neskubekit taip Mokytojau. Pirma as turiu ismokti klausti Jusu. 🙂
Burgis, 2010-08-17 16:07:22
Smokai, būsiu atkaklus: kiek yra taškų? Spėju, kad šeši – trys taškai sudaro vieną trikampį, kiti trys – kitą. O kur piramidė? Ko nesupratau?
Burgis, 2010-08-17 16:08:54
Aurelijai: pavaikščiojau po internetą ieškodamas, gal ir mane kas įrašė… Pasijuoktumėte.
Ursus, 2010-08-17 16:23:30
Itariu, kad abieju “menamu” pirmadziu virsune yra (0;0;0). 🙂
Smokas, 2010-08-17 16:54:37
atsiprašau (mokausi po truputį), pamiršau balto ir juodo taško koordinates. Dabar visos koordinates kartu ir gaunasi jau nebe piramidės:
- figura
X Y Z
R(0,6097; 0,3111; 0,0195)
G(0,2053; 0,6257; 0,0609)
B(0,1492; 0,0632; 0,7446)
W(0,9505; 1,0000; 1,0891)
Blk(0 ; 0 ; 0 ; 0)
- figura
R(0,4625; 0,2428; 0,0112)
G(0,3563; 0,6749; 0,0709)
B(0,1455; 0,0823; 0,7429)
W(0,9642; 1,0000; 0,8249)
Blk(0; 0; 0)
Kokio didžiausio skersmens sfera telpa šių figūrų susikirtime ir kokios jos centro koordinatės ?
Ačiū, kad iškvotėte. 🙂
Burgis, 2010-08-17 19:55:05
Na, Smokai, dabar jau lyg ir aišku… Sprendimas man neatrodo sunkus, bet ilgas ir gremėzdiškas. Gal kas nors žino trumpesnį kelią, bet aš rašyčiau susidarančių plokštumų lygtis, ieškočiau jų sankirtų (tiesių ir taškų) ir pagaliau, suvokęs sankirtoje gautą kūną, rasčiau tašką, nuo kurio iki visų to kūno plokštumų yra vienodi atstumai. tai ir būtų sferos centras.
Bet gal čia yra koks aiškus atskiras atvejis? Reikėtų, pavyzdžiui, Mathcad programa pamatyti tą sankirtos kūną…
Ursus, 2010-08-17 22:21:38
Kunas sankirtoje gaunasi visikai kreivas. Neturiu minciu kaip rast taska, vienodai nutolusi nuo visu plokstumu.
Burgis, 2010-08-17 22:48:12
Ursus: pradėkime nuo paprasto pavyzdžio. Kokio dydžio sfera telpa tetraedre, apribotame koordinačių plokštumomis ir plokštuma x+y+z=1? Tarkime, kad tos sferos centras yra taške O(a;b;c). Suprantama, kad to taško atstumas d iki koordinačių plokštumų yra atitinkamai a, b ir c, o tai reiškia, kad turi būti a=b=c. O iki ketvirtos plokštumos tas atstumas yra d= (a+b+c-1)/SQRT(3) – yra tokia taško atstumo iki plokštumos formulė. Taigi d=(3d-1)/SQRT(3). Iš čia ir gauname d. Įdomu, tiesa?
Ursus, 2010-08-17 23:07:15
Taip, pasakyčiau netgi paprasta. Bet duotu atveju turim 10briauni, panasu i aplaužytą ryklio dantį. 🙂
Burgis, 2010-08-18 08:35:10
Ursus: teks kreiptis į stomatologus… Tingiu vasarą spręsti tokius uždavinius, tingiu…