Gimnazija vėl veikia! Klasės pilnos moksleivių!
Tai žadina viltį, kad trečiadienį ir ketvirtadienį 15.15 ateis ir penktokų. Jie gaus ankstesnėje temoje paskelbtą namų darbą (žinoma, ir dar šio to…). Tačiau manau, kad penktokus reikia šiek tiek “nukreipti”: apie žvaigždės smaigalio kampo dydį reikėtų sužinoti vien tik remiantis tuo, ką žino penktokai, – trikampio vidaus kampų suma lygi 180 laipsnių. Jokių įbrėžtinių į apskritimą kampų, jokių centrinių kampų, jokių lygiašonių trikampių ir pan.
Be to, parodysiu, kad tikslaus brėžinio nereikia – čiumpi popieriaus, “iš rankos” nubrėži kreivą šleivą žvaigždę ir imi nagrinėti trikampius, kampus…

Tęsinys – po dviejų savaičių.
Atsakymai
Audrius, 2009-11-30 12:42:37
36 laipsniai.
viski kas yra gretutinis kampas reikia zinoti 🙂
D., 2009-11-30 12:47:12
Audrius: visgi lietuvių k. reikia mokėti 🙂
Burgis, 2009-11-30 12:55:54
Audriui: ne, tokių baisių terminų (gretutinis kampas…) žinoti nereikia, bet matyti akivaizdžius dalykus būtina!
Tai tikra problema: mokykloje moko kuo greičiau viską pavadinti, neduodami žmogui priprasti prie ko nors akimis ar ausimis… Kiek naujų, gerų, tikslių žodžių atsirastų, jei moksleiviams ir studentams būtų leista patiems ką nors pavadinti! Nepamenu, kuris kalbininkas išgirdo, kaip valstietis apie jautį pasakė: “jis dar mokinys, todėl sunku arti…” Taip lietuvių kalboje atsirado žodis “mokinys”!
Paulius, 2009-11-30 21:00:57
Pabandžiau paprasčiau pažiūrėti – jei nukirptume bet kurias dvi viena prieš kitą esančias (na svarbu, kad nebūtų viena šalia kitos) žvaigždės atšakėles ir sudėtume jas kaip delionę į tarpą tarp kitų dviejų atšakėlių, tai gautume jau nebe žvaigždę, o gražų trikampį. Kaip žinia, visi 5 lygūs kampai tuomet sudarys 180 laipsnių.
Burgis, 2009-11-30 22:21:03
Pauliui: įtariu, kad pasiūlėte puikų sprendimą, bet nieko nesupratau… “…gautume trikampį… visi 5 kampai…”. Trikampis yra su trimis kampais.
Paulius, 2009-12-01 15:42:43
Priglaudus nukirptų atšakėlių kampus (tuos, kuriuos reikia rasti) prie bet kurių kitų šalia esančių atšakėlių taip, kad nukirptųjų ir tų šalia esančių atšakėlių kampai būtų šalia, atsitiks taip, jog užsipildys erdvė esanti tarp tų šalia esančių atšakėlių. Jei iš tiesų taip padarytume, pamatytume, jog turime nebe pentagramą, o gavome trikampį, kurio kampai yra 2x, 2x ir x laipsnių.
Sunku parodyti negrafiškai, bet nesu profesionalas braižyme kompiuteriu…
Burgis, 2009-12-03 11:00:40
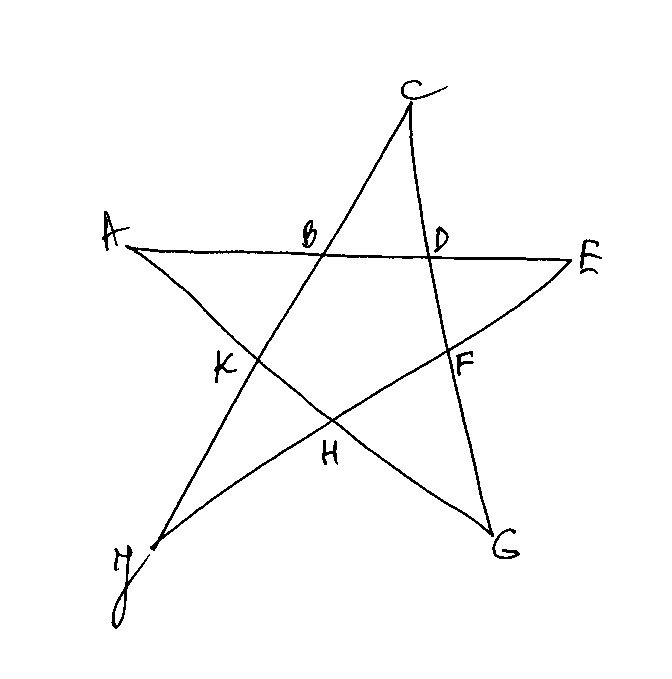
Pauliui: labai smalsu! Bet nesuprantu… Įdedu dar vieną brėžinėlį, gal galėtumėte dabar parašyti maždaug taip: nukerpame ties KB ir HF; kraštinę AB priglaudžiame… ir pan.
O gal kuris nors skaitytojas suprato ir gali “išversti”?
O., 2009-12-03 22:14:07
Nukerpam trikampiukus KAB, BCD, DEF, FGH,HJK, ir suglaudžiame:
AB su BC, CD su DE, EF su FG, GH su HJ, JK su Ka…
Burgis, 2009-12-04 11:10:04
O.: ir vėl nieko nesupratau… Penkis kampus suglaudžiame taip, kad visų smaigaliai būtų viename taške? Gausime kampų “puokštę”, ką ir kaip toliau įrodysime? Ar posakis “suglaudžiame AB su BC” reiškia, kad ne A sutaps su C, o A sutaps su antrojo kampo B? Kas toliau?
Valdas, 2009-12-04 16:50:58
Šį kartą neiškenčiau neįkišęs savo trigrašio nors iki šiol buvau tik stebėtojas.
Šį uždavinį galima išspręsti ir lygčių sistema, nežinau ar penktokai moka tokias spręsti….
Štai paimkim žvaigždės „spyglį“ – JKH. Pažymėkime smailiausią kampą x, du kitus kampus – y.
Tada x + 2y = 180
Matau dar vieną trikampį ADG. Matydamas jį galėčiau pasakyti, kad 2x + (180 – y) = 180.
Taigi turiu tokią lygčių sistemą
x + 2y = 180
2x = y
Iš čia
5x = 180
x = 36
Burgis, 2009-12-04 17:49:35
Valdui: gerai, bet gana įmantriai…
Rasa, 2009-12-05 16:00:33
Tas berniukas Paulius gražiai paskaičiavo. Na paimkim ir mintyse nukarpykim visus 5 spygliukus, t.y. tuos trikampiukus, liks tik penkiakampis vidurys, jis nereikalingas 🙂 Sudėkim tuos spygliukus taip, kad mums reikalingi smaigaliukai sueitų į vieną tašką. Gausis vėduoklė- apačioj tiesi linija- 180 laipsnių. Vėduoklė susidarys iš 5-ių gražių vienodų į viršų platėjančių trikampių, o tie kampai, kurių mums reik ir sudarys bendrai tuos 180 laipsnių. Tada padalinam iš 5 ir va! 36 laipsnių smaigaliukas!
Rasa, 2009-12-05 16:04:23
Oi, paskaičiau, Paulius lyg ir kitaip ten darė 😛
Burgis, 2009-12-05 16:13:29
Rasai: žinau, Jūs neįsižeisite, jei pakartosiu: yra logika, yra matematinė logika ir yra moteriškoji logika. Jos vyrams nesuprasti! Jūsų įrodymas iškart įstrigs, kai reikės paaiškinti, kodėl ta “vėduoklė” sudaro ištiestinį kampą – 180 laipsnių…
Rasa, 2009-12-05 16:32:17
Tai jau Jūs per daug norit! Iš pradžių tik rasti kampą reikėjo, o jau dabar ir kad įrodinėt užsimanėt :)))))) Ir klausimas ne iš tos pusės 🙂 Ne “kodėl” ta vėduoklė sudaro 180 laipsnių, o todėl ji gaunasi 180-ies, kad kampiukas 36-ių, kitaip gi nesigautų! :)))) Aš tai manau, kad ir Einšteino teorijos ne visos įrodytos :))))))))
Tai čia tik tokiai žvaigždei tinka, tai nukarpykit, sudėkit ir įrodyta! :))))))
Rasa, 2009-12-05 18:07:20
Netinka mat, moteriškai. Negaliu valgyt ramiai gamint, žvaigždės akyse mataruojas…
Gerai, bandom kaip Einšteinas, protingiau…
Žiūrim į Burgio trikampukus viršuj. Matot užuominą: vidurinis penkiakampis “sudarytas” iš 3 trikampių. Jų kampų suma 180×3=540. Kadangi šio penkiakampio kampai lygūs, padalinam iš 5 ir gaunam, kad vienas kampas 108 laipsniai. Dabar kad būtų lengviau paaiškint žiūrim, vaikai, į apatinį brėžinį 🙂 Ir ką mes čia turim? Ogi sprendimuką! Jei kampas KBD ir BDF yra po 108 laipsnius, tai anoj, mūsų spygliuko pusėj, kampai CBD ir CDB bus po 180-108=72 laipsnius. Vadinasi ponai ir ponaičiai, jei trikampio kampų suma 180, tai mūsų mielas smaigaliukas bus: 180-72-72=36 laipsniai.
Ar dabar jau gerai, ar dar ne?
Burgis, 2009-12-05 18:33:30
Bingo! Rasa išsprendė aiškiai, paprastai, teisingai, griežtai tiksliai! Va, ką reiškia erzinti moteris…
Raimundas Zabarauskas, 2009-12-06 17:50:56
Grakštus sprendimas, bet ar penktokiškas?
Man lengviau rasti CDB taip: eidamas išilgai penkiakampio (DBKHF) padarai penkis posūkius ir vėl atsisuki ten pat. Vadinasi, kaskart sukiesi po 360/5=72 laipsnius.
Tada belieka tas trikampis.
Burgis, 2009-12-06 20:38:36
Raimundui: tai kad penki posūkiai yra po 108 laipsnius… Bet jei net ko nors nesupratau, šis sprendimas paprastumu neprilygsta Rasos sprendimui. Bet tegu sprendžia penktokai.
Raimundas Zabarauskas, 2009-12-07 07:31:19
Burgiui: siūliau judėti išilgai penkiakampio (DBKHF), o ne visos žvaigždės (CJEAG).
Žiūrėjau į šį sprendimą šiek tiek informatiko akimis: yra tokio pragramavimo kalba/aplinka LOGO, kurioje mokiniai (penktokai?) piešia apskritimus maždaug taip:
KARTOK 360 [ PR 1 KR 1]
„Vėžliukas“ 360 kartų brėžia vienetinio ilgio brūkšnelį ir pasisuka 1 laipsniu. Griežtai šnekant tai ne apskritimas, o trys šymtai šešiasdešimtkampis. Penkiakampį gali taip:
KARTOK 5 [PR 100 KR 72]
Ši logika (180-360/5) universaliai tinka bet kurio taisyklingo daugiakampio viršūnės kampo radimui…
Burgis, 2009-12-07 09:42:55
Raimundui: vakar prieš užmigdamas jau supratau, ką Jūs turėjote galvoje sakydamas “padarai penkis posūkius” ir pripažįstu, kad sprendimas elegantiškas, “informatiškas”… Bet aš vis tik aiškinu taip, kaip Rasa.
Beje, gal kitiems bus įdomi tokia pastaba: pridėjus vieną daugiakampio kampą, figūros vidaus kampų suma padidėja 180 laipsnių, nes galima nubrėžti dar vieną trikampį (žr. pirmą brėžinį).
Paulius, 2009-12-07 19:36:18
Atsiprašau, kad buvau dingęs. Su įdėtu brėžiniu, manau, man bus lengviau paaiškinti. Tik nežinau, ar mano atsakymas bus teisingas.
Paimkime ir nukirpkime trikampiukus ABK ir DEF. Dabar pažiūrėkime į brėžinio apačią – galime įsivaizduoti numanomą trikampį JHG. Į jį turėtų puikiai įsikomponuoti tie nukirpti maži trikampiukai. Įdėkime juos į tą numanomą trikampį JHG: taip, kad B ir D kampai liestųsi su H kampu, kampas A liestųsi su kampu J, o kampas E – su kampu G.
Ir šitaip iš žvaigždės gauname trikampį, kurios viršunės yra taškas C, bei taškų E ir G, bei taškų A ir J “sumos” (nežinau, kaip pavadinti). Kadangi žinome, jog kampai C, E, G, A ir J yra lygūs, 180 padalinsime iš 5 ir gausime teisingą atsakymą.
Bet tai tik prielaida. Nesu įsitikinęs, ar pavyktų taip lengvai tuos trikampiukus iškirpti ir įkomponuoti.
Burgis, 2009-12-09 09:07:04
Pauliui: “Į jį turėtų puikiai įsikomponuoti tie nukirpti maži trikampiukai.” Taip puiki proza, bet ne matematika…
Burgis, 2009-12-09 09:07:56
Pauliui: beje, Pauliau, ar Tu ne tas sumanusis Paulius iš Klaipėdos?
Eglė, 2009-12-09 15:54:40
Rasos sprendimas tikrai paprastas. O iš kur gaunamas teiginys “kadangi šio penkiakampio kampai lygūs”. Nuraminkit mane, nes ir man žvaigždės akyse jau kelinta diena:)
Paulius, 2009-12-09 15:59:44
Tiesa, šie trikampiai neįsikomponuoja, žioplai pasakiau. Bet jie gali persidengti – vis tiek gautume didelį trikampį, kurio kampų suma būtų lygi penkių atšakėlių kampų sumai.
Jei ir tai nėra aišku/įtikinama/teisinga, pasuoju.
Aš iš Šiaulių – Didždvario gimnazija.
Rasa, 2009-12-10 08:26:11
Ponas Burgi, čia Eglė Jūsų klausia tikiuosi? Nes kas gi matematikos profesorius po galais, Jūs ar aš? :)))))) Tai Jūs ir paaiškinkit. Beje, vaikai sako, kad normalus penktokas puikiausiai išspręstų ir kaip Valdas sakė, lygčių sistema.
Paulius, 2009-12-10 17:58:43
Rasa, manau tai vyksta ne dėl to, kad tiesiog sužinotume atsakymą. Kad ir koks būtų klausimas, ka ir kokios būtų aplinkybės, jis turbūt turės bent vieną logiškai paaiškinimą atsakymą. Sakome ne dėl atsakymo, o dėl to, kad ir patys smegenis pakrutintume, kad įsitikintume, jog ne visada yra toks atsakymas, koks iš tikrųjų gali pasirodyti. Na ir kas, kad penktokas išspręstų – gal galime tam penktokui parodyti, jog čia nebūtinai reikia lygčių sistemos? 🙂
Rasa, 2009-12-10 21:07:30
Pauliui: suprantu 🙂 Ir buvo labai smagu pasvarstyti, nes matematikos mokiausi prieš milijoną metų :))) Ir buvau primiršus net tai, kad trikampio kampų suma 180 laipsnių 🙂 Net susigėdau 🙂
Burgis, 2009-12-14 09:36:31
Peržiūrėjau penktokų darbus. Tik vienas atsakymas (45 laipsniai) neteisingas, visi kiti – 36 laipsniai – teisingi. Bet nė vienas mano geras žmogutis NIEKO nepaaiškino, neįrodinėjo! Tik viena mergaitė nubraižė čia minėtą “vėduoklę”, išskleistą 180 laipsnių (kodėl?) kampu.
Kodėl neįrodinėjo, neaiškino ne tik šios užduoties? Nes nebuvo klausta! Vaikai įpratę prie testų: pažymėk, įrašyk, pabrauk… Vargo mokyklos vaikai…
Atsakau Eglei ir Rasai: “kadangi šio penkiakampio kampai lygūs” – žinoma, reikėtų įrodyti, nors tai ir akivaizdu! Bet matematikoje (geometrijoje) įrodinėjant retai pradedama nuo trijų Euklido postulatų. Dažniausiai sutariama, kad kažkas jau įrodyta, pavyzdžiui, kad trikampio vidaus kampų suma lygi lygi 180 laipsnių ir pan. Pavyzdžiui, šiuo atveju bene trumpiausias įrodymas apie kampo dydį būtų pasinaudojant teorema, kad įbrėžtinis kampo dydis laipsniais yra pusė lanko, į kurį jis remiasi, laipsnių: 360:5=72:2=36. Bet penktokai to nežino!
Taigi penktokams leistina sakyti, kad viduje esantis penkiakampis yra su vienodais kampais todėl, kad matome… Septintokai sakytų: visi žvaigždės viršūnių kampai lygūs, todėl matome lygiašonių trikampių, leidžiančių įrodyti penkiakampio taisyklingumą…
Mamoms ir tėčiams: bijokite, kad mokykla testais nužudys jūsų vaiko polinkį rašyti ir kalbėti sakiniais, įrodinėti, motyvuoti!
Džiaugiuosi, kad į klausimą “Ar Mildutė nori miegelio?” sulaukiu atsakymo: “Ne, Mildutė dabar visai nenori miegelio!”
neringa, 2010-11-05 18:05:01
labai paprasta matosi kad 36 laipsniai kai truputy pamatuoji nu i viskas po visos cia matematikos
neringa, 2010-11-05 18:06:21
geras uzdavinys daug galvoti….