Po daugelio metų mane perkėlė dirbti į Statybos fakultetą. Labai džiaugiuosi, nes tai naujas potyris. Pažįstu keletą labai išsilavinusių žmonių, kadaise baigusių šį fakultetą. Nekantraudamas laukiu susitikimo su „kitokiais“ studentais. Suprantu, kad dabar vasara, bet gal kas nors iš jų norės pasikartoti pirmo kurso temą „Integralai“? Pateikiu kitoje šios svetainės temoje minėtą integralą, jis man patinka…
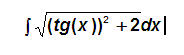
Čia galiu iš anksto atsakyti į kokius nors intymius klausimus. Pavyzdžiui, kiek paskaitų reikia aplankyti, kad išlaikytum egzaminą? Kurioje eilėje sėdinčius dėstytojas labiausiai mėgsta? Nuo ko dėstytojas patiria alergiją?
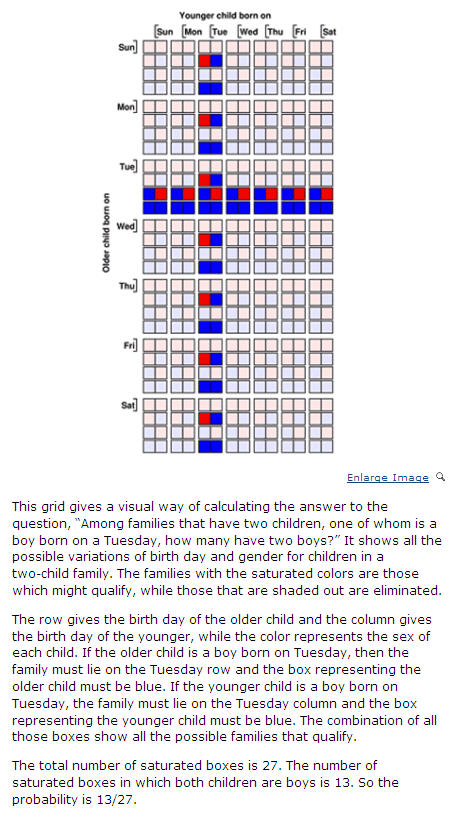
P.S. Čia Mindaugo pateikto uždavinio grafinis sprendimas. Bet vėl kartoju – būtinai perskaitykite visą tekstą!
Atsakymai
SIMAS, 2010-08-10 22:13:13
Ponas burgi nepamirskite elektriku 🙂
Burgis, 2010-08-10 22:16:55
SIMUI: „Man ponas sako – aš einu“ (V.Šekspyras)
PaBandyk, 2010-08-11 00:26:31
nejau pamirsite ?!!!
Burgis, 2010-08-11 08:32:13
Mieli kolegos studentai,
aš prisimenu vos vieną kitą studentą, kurį mokiau per tuos 38 metus, bet gerai prisimenu darbo kiekviename fakultete jausmą… O dirbau Mašinų gamybos, Radioelektronikos, Automatikos, Elektros, Tarptautinių studijų, Skaičiavimo technikos fakultetuose. Ir štai dabar – Statybos fakultetas! Deja, elektrikai, aš nesu tas, kuris galėtų rinktis – man parenka, kur ir ką dirbti. Aš nesipriešinu – kiekvienas darbas garbingas ir įdomus. Ačiū jums, elektrikai, už bendravimo metus!
Vytautas, 2010-08-11 10:30:54
Tai ačiū Jums už metus su elektrikais 😉
Mindaugas, 2010-08-14 20:49:36
Labai jau nuobodus uždavinys…integralai, formulės, fe… Aš va siūlau kur kas įdomesnį išspręsti:
“Turiu du vaikus, vienas iš jų – berniukas, gimęs antradienį. Kokia tikimybė, kad kitas mano vaikas irgi yra berniukas?”
Rezultatas turėtų nustebinti…
Burgis, 2010-08-14 21:48:33
Mindaugui: tai visai įdomus uždavinys! Reikia statistikos. Teigiama, kad tikimybė gimti berniukui yra 0,51. Iš to Maltuso teorija padarė išvadą, kad karai neišvengiami – vyrų yra daugiau… Galima pagalvoti, kad tikimybė gimti berniukui IR berniukui yra 0,51*0,51. Bet taip nėra! O kaip yra?
giedrius m, 2010-08-15 23:21:55
Lygiai ta pati, 0.51 %.
Beje, išgyventi iki 20 metų berods yra didesnė tikimybė mergaitėms. Berniukai yra mažiau atsparūs ligoms, patiria daugiau traumų.
Burgis, 2010-08-16 15:24:37
Giedriui M.: duokime žmonėms pagalvoti: šeimoje auga devyni berniukai. Kokia tikimybė, kad ir dešimtasis, kuris jau studijuoja, yra berniukas? 🙂
Mindaugas, 2010-08-16 22:59:33
Priimkime kad jei turiu 2 vaikus, tai vienodai tikėtina, kad jie gimė berniukas+berniukas, berniukas+mergaitė, mergaitė+berniukas ar mergaitė+mergaitė. Jei turiu 1 berniuką,, tai kombinacijos mergaitė+mergaitė tikimybė=0, o likę variantai vienodai tikėtini (tikimybė 1/3). Kitaip tariant, jei vienas iš vaikų – berniukas, tikimybė 1/3 kad ir kitas bus berniukas. Bet….neskubėkim
X=berniukas gimęs antradinį
P(X|bernbern) = 1/7 + (6/7*1/7) = 13/49
P(X|bernmerg) = 1/7
P(X|mergbern) = 1/7
P(bernbern) = P(bernmerg) = P(mergbern) = 1/3
P(X) = (1/7 + 1/7 + 13/49)/3 = 9/49
Naudojam Bayes’o teoremą:
P(bernbern|X) = P(X|bernbern)*P(bernbern)/P(X) = 13/49 * 1/3 * 49/9 = 13/27
O tai ne tas pats kas 1/3!
Daugiau detalių čia: http://science.slashdot.org/story/10/06/28/2221252/The-Tuesday-Birthday-Problem?from=rss
Burgis, 2010-08-17 08:57:39
Mindaugui: parašyčiau Jums… tik 9 balus. Vieną balą pridėčiau vien už tai, kad pateikėte nuorodą. Visiems rekomenduoju ATIDŽIAI perskaityti viską, kas ten parašyta!
Mindaugas, 2010-08-17 16:09:16
9 balai – visai neblogas pažymys 😉
Gal pakomentuotumėte plačiau (galima ir atskirame straipsnyje)?
Burgis, 2010-08-17 16:29:45
Palaukime, Gerb. Mindaugai, turėtų atsiliepti matematikos grandai… Balą atimu todėl, kad straipsnyje nurodytos įvairios versijos, o Jūs pateikėte tik sensacingiausią. Sekite mano diskusiją su Smoku kitoje temoje – labai aiškiai matyti, kad galima gauti įvairius atsakymus priklausomai nuo to, kaip paklausi ir ką turėsi galvoje…
Daiva, 2010-08-19 20:08:01
Pavydžiu jūsų artimo ir atviro bendravimo. Ir džiaugiuosi, kad atsitiktinai čia atėjau. O gal ir visai neatsitiktinai 🙂 Programavimo uždavinį persiunčiu savo sūnui, gal jis pagyvins diskusiją 🙂
Jonas, 2011-04-28 01:30:44
Sveiki, radau jūsų svetainėjė šį įdomų uždavinį su integralu. Pats dėstau pratybas studentams, tai buvo smagu pasigalinėt su juo:
P.S. Kažkodėl iš pirmo karto komentaro neįkėlė.