
Lysvę sukasiau. Kerpes, samanas pavaliau. Pavalgiau. Paskaičiau. Parašiau. Nufotografavo. Dovanėles anūkėliams parengėme.
*
Vis tiek kažko trūksta? Aišku, ko! Matematikos! Negalima praleisti treniruočių.
Štai jums keturi 2007 metų VBE užduočių sprendimai. Pasirinkau visai skirtingus uždavinius. Surinkau 13 taškų – egzaminą išlaikiau! Pastebėkite, kad lengvesnius uždavinius su panieka praleidau…
***


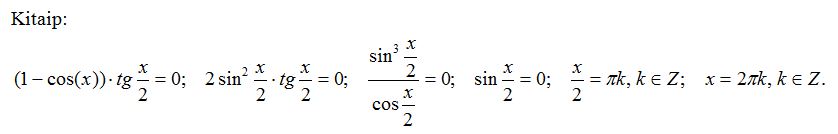
Atsakymai
Burgis, 2015-04-09 19:37:50
Balsuok teigiamai, nes kitaip daugiau neskelbsiu… 🙂
Sokolovas, 2015-04-09 19:46:32
Gerb. Burgiui
13 uždavinio atsakymas kitoks. Ne pi k, o 2 pi k.
Tangento apibrėžimo sričiai nepriklauso pi k, kai k- nelyginis.
Burgis, 2015-04-09 20:34:53
Sokolovui: o, ačiū, pražiopsojau!
qwerty, 2015-04-09 20:45:55
Aha, kad man vaikystėje būtų tekus laimė turėti tokius matematikos mokytojus, tai gal suprasčiau ją dabar, ech. Bet aš ir geras buvau, nesupratau matematikos, algebros beigi geometrijos, todėl ir nesimokiau iš pykčio) Užburtas ratas buvo. Mokytojai, ką jūs būtumėte darę su manim tokiu?
Burgis, 2015-04-09 20:47:02
qwerty: aš mokiau penktokus, jų visokių būdavo. Visaip ir mokiau…
ema, 2015-04-09 20:48:37
Man prie sirdies labiau lyrika
Burgis, 2015-04-09 20:53:06
emai: taip, aš jau laukiu, kada man mūzos padiktuos eilėraštį…
qwerty, 2015-04-09 21:08:43
Kad kas man pasakytų, kur šitie uždaviniai, jų sprendiniai yra naudojami praktiškai.Kad suprasčiau.
Burgis, 2015-04-09 21:09:55
Supykau ant savęs už klaidą, tai įdedu kitokį, gal saugesnį, tryliktojo uždavinio sprendimą…
Burgis, 2015-04-09 21:14:31
qwerty: aš žinau, aš žinau!…
-
Praktiškai jie labai praverčia laikant VBE, gaunant geresnį atestatą ir įstojant į geresnį universitetą.
-
Tokiems, kaip aš, kaip Jūs jie labai praverčia kaip svarmenys, krepšinio kamuolys, teniso raketė… Tik tiek, kad ne raumenims, o smegenims. Bet veikia analogiškai – lėčiau sensti.
qwerty, 2015-04-09 21:17:19
Bet pirmame variante parašėte kaip aiškiaregis: “…gal pabaigoje bus komplikacijų?”
qwerty, 2015-04-09 21:19:44
Ma nepraverčia, nes žiūrau į šias formules, kaip ožys į baltus vartus. Ir taip jau mani savivertė žemiau plintuso, o dar kai į šituos uždavinius paspoksau…)
qwerty, 2015-04-09 21:23:18
Tinklaraštininke, ačiū už atsakymą. Bet aš galvoje turėjau, kur šitie dalykai moksle, statybose, inžinierijoje, etc. yra taikomi. Suprantu, kad taikomi, bet įdomu kur ir kaip?Bent vienu pavyzdžiu.
Sokolovas, 2015-04-09 21:26:59
DĖL KITOKIO BŪDO
Gerb. Burgiui.
Sąlygoje buvo kitokia lygtis.
Ten ne toks ženklas sąlygoje.
Juk buvo ( 1 + cos(x/2)…..
Spręsdami kitu būdu, taikysime kitokią laipsnio mažinimo formulę, ir gausime lygtį
2 cos(x/2) sin(x/2) =0, kai cos(x/2) nelygu nuliui. T.y. sinx = 0, kai x nelygu pi + 2 pi k.
Tad šis būdas irgi nėra “saugus”
Sokolovas, 2015-04-09 21:29:12
Turėjau omeny, kad buvo ( 1 + cos x ), o ne
(1 – cos x)….
Toliau kaip mano ankstesniame tekste…
Rasa, 2015-04-09 21:33:36
Qwerčiui: nu aš pabandysiu tau papasakot 🙂 Pats žinai, vis suku galvą apie malkas, tai va. Žiūrėk. 12-am uždaviny sukrauta rastų rietuvė ir reikia apskaičiuoti kiek realiai malkų (kietmetrių) nusipirksi. O daug kas pardavinėja erdmetriais, t.y. į kainą įskaičiuoti ir oro tarpai, va tie juodai užtušuoti. Tai jei būtum geras matematikas ir netingėtum skaičiuot, niekas tavęs apgaut negalėtų, nes pirkdamas malkas erdmetriais, tu suskaičiuotum, kiek užima oro tarpai, o kiek grynos medienos gausi :))))))) Žinoma, realiai tai supaprastinta ir žmonės daugina tik iš tam tikro koeficiento, bet juk būtų galima pritaikyti? 🙂
Burgis, 2015-04-09 21:36:22
Sokolovui: tikrinau Jūsų budrumą… 🙂 Sveikinu, viską pastebite! Nors ir Jūs klystate, ne (1+cos(x/2)) buvo, o (1+cos(x)). Bet juk jokio principinio skirtumo nėra, norėjau tiesiog parodyti kitą kelią…
Sokolovas, 2015-04-09 21:41:52
DĖL TRIGONOMETRINIŲ LYGČIŲ TAIKYMO
Įsivaizduokite, kad Jūs sukatės “apžvalgos ratu”, kurio sukimosi periodas 10 min. Kokiais laiko momentais Jūs būsite aukščiausiame rato taške?
Akivaizdu, jog 5 min., 15 min., 25 min., ir t.t. Trumpiau-
5 + 10k, kur k yra sveikasis skaičius.
O jei norite rasti visus laiko momentus, kuriais jūs būsite kitokiame aukštyje? Tuomet jums ir padės trigonometrinė lygtis.
Tepadeda Jums ! 🙂
Burgis, 2015-04-09 21:42:38
qwerty: atsakau rimtai: norėdamas tapti inžinieriumi, pavyzdžiui, elektroninės technikos inžinieriumi, koks aš ir esu (buvau), turi baigti universitetą. O universitete yra daug uni- mokslų, visai arba beveik visai nesusijusių su profesija. Pavyzdžiui, kam mums dėstė braižomąją geometriją, medžiagų atsparumą, teorinę mechaniką? Tam, kad būtume uni-. Tam, kad išmoktume mąstyti moksliškai: tiksliai, logiškai, kūrybingai, tikslingai, asociatyviai, etc. O visuose tuose moksluose yra nemažai matematikos. Žinoma, tokių uždavinių, kaip čia parodžiau, gali ir nepasitaikyti (nors tas ploto radimas tarp skritulių gali būti vadinamas klasika…), bet sprendimo principai yra gana bendri. Kita vertus, pati matematika yra mąstymo lavinimo įrankis. O kaip be mąstymo šiuolaikiniame pasaulyje? Nuobodu…
qwerty, 2015-04-09 21:43:34
Rasa))), na o įžymusis 13 uždavinys? Kaip su jo sprendinių praktiniu panaudojimu?
Sokolovas, 2015-04-09 21:44:00
Gerb. Burgiui
O taip, aš irgi klystu…Beje, galėjau ir nepastebėti. Nes buvau į filmą persijungęs. Bet…nuojauta pakuždėjo…;)
qwerty, 2015-04-09 21:47:08
…Sprendimo principai yra bendri…Gerą dalyką sužinojau. Atsiminsiu.
qwerty, 2015-04-09 21:48:09
O 13 uždavinio, koks sprendimo principas?
Rasa, 2015-04-09 21:53:16
Qwerčiui: O ką 13-as? 13-as tai ką… Apie 13-ą pasakyčiau: “tai matai, kaip čia įdomiai gaunasi…” 😛
qwerty, 2015-04-09 21:59:09
Tinklaraštininkas dar kiek paaiškina, bet irgi labai nedaug. Nenori prasidėt, nes jaučia, kad užversčiau iki galvos su savo kodėl ir kaip.Man įdomu.
Sokolovas, 2015-04-09 22:01:56
DAR VIENAS (13) LYGTIES SPRENDIMO BŪDAS
Algebrizuojame trigonometrinę lygtį keitiniu
t = tg(x/2).
Kadangi cosx=(1- t kvadratu)/ ( 1 + t kvadratu), tai
lygtis keičiama algebrine lygtimi:
2t/ ( 1 + t kvadratu) = 0.
Tuomet t =0, t.y. tg(x/2)=0, x/2 = pi k,
x= 2 pi k. k priklauso Z.
Sokolovas, 2015-04-09 22:16:19
IR DAR DĖL “TAIKYMO”
Aš išpažįstu tokį tikėjimą- jei uždavinys gimė, jei jis apsireiškė mums, tai ties tuo slypi didžioji prasmė, kur kas galingesnė už pragmatizmą ar jo kildinamą skubotumą.
Uždaviniai stipresni už mus! Mes galime pretenduoti tik į dalelę tos nuostabios pažinimo Laimės…
O kas yra Laimė? Juk tai yra gebėjimas nepaliaujamai ieškoti atsakymo į klausimą KĄ DARYTI. Ir kartu nepretenduoti į visažinio vaidmenį. Ir todėl…
MATEMATIKA- NE TARNAITĖ. MATEMATIKA- KARALIENĖ. O uždaviniai- gvardija jos!…
Mokytoja, 2015-04-09 22:58:38
Patarkite kaip racionaliau išspręsti uždavinį:
teatro ložėje vienoje eilėje yra 6 vietos. Pertraukos metu žiūrovai gali išeiti į holą iš abiejų pusių. Kokia tikimybė, kad bent vienas žiūrovas, norėdamas išeiti, turės paprašyti praleisti kurį nors iš šioje eilėje sėdinčių žiūrovų?
Sokolovas, 2015-04-10 07:41:33
Mokytojai
Iš pradžių randame priešingo įvykio (visi 6 išeis “be kliūčių” ) tikimybę:
(2/6)(2/5)(2/4)(2/3)(2/2) = 32/720=2/45
Tuomet mus dominančio įvykio tikimtbė
1- (2/45)=43/45
Andrius, 2015-04-10 07:51:48
Įdomus nuotraukos aprašas 🙂
“Burgis Bronius, buvęs KTU gimnazijos dir.”
Gediminas, 2015-04-10 11:19:54
Ačiū, Burgi, ačiū. Labai smagu būtų ir dažniau pamatyti tokių įrašų. Gal nors kartą per savaitę…
Sokolovas, 2015-04-10 11:58:11
Besidomintiems
ŠIANDIEN “ŠIMTADIENIS”. LIKO 265 DIENOS…KAS?
Jums padės uždavinys:
64 žmonės, susitikę, sveikinasi rankų paspaudimais. Kiek bus iš viso rankų paspaudimų?
Rasa, 2015-04-10 12:16:07
Sokolovui: 2016!
aina na, 2015-04-10 12:26:27
3969
Sokolovas, 2015-04-10 13:38:14
Rasa šaunuolė! Puikiu !
mokinys, 2015-04-10 14:41:18
gal galite paaiškinti tą sandaugą (2/6)(2/5)…, ačiū
qwerty, 2015-04-10 14:53:58
Rasa, tu moki normaliai ir suprantamai paaiškinti. Paaiškink, kaip gavai atsakymą. Nuo ko pradėjai?Kokį principą taikei sprendimui? Nes dažnai Sokolovas ar tinklaraštininkas taip mandrai aiškina, kad tam jų aiškine vėl klausimai ir neaiškumai.
mokinys, 2015-04-10 14:58:06
manau padėjo žodis ŠIANDIEN
Sokolovas, 2015-04-10 15:17:53
Mokiniui
Yra šešios vietos, dvi- iš kraštų. Pirmasis išeinantis, kad nereikėtų kitiems jo praleisti, turi pakilti būtent iš tų vietų. Tikimybė 2/6.
Jam išėjus, lieka penkių žmonių eilė. Tikimybė, kad kitas pakils iš šios ( sumažėjusios) eilės krašto ( kurių yra du) lygi 2/5. Ir t.t…
Tikimybė, kad nei vienam nereikės prašyt kitų praleisti, gaunama, remiantis priklausomų įvykių sankirtos ( sandaugos) tikimybės skaičiavimo taisykle.
Taip ir gaunama sandauga (2/6) (2/5) (2/4)….
Vilniete, 2015-04-10 15:40:26
O kaip su tais ranku paspaudimais? Net nesiimu speti:-)
Sokolovas, 2015-04-10 16:11:53
Vilnietei
Sumodeliuokim paprastesnę situaciją:
Nusibrėžkite apskritimą, jame pažymėkite 6 taškus. Dabar juos visus sujunkite atkarpomis ( poromis). Jei nepraleisite nei vienos atkarpos, gausite 15 atkarpų ( 6 kraštines bei devynias įstrižaines).
Ką tai reiškia? O štai ką. Jei susitiks 6 žmonės, ir vieni su kitais sveikinsis rankų paspaudimais, tai iš viso bus 15 rankų paspaudimų. Juk viena atkarpa- vienas pasisveikinimas!
Sokolovas, 2015-04-10 16:28:07
Vilnietei
Nepraeina komentaras su paaiškinimo tęsiniu…
Sokolovas, 2015-04-10 16:34:58
Vilnietei tęsinys
Viskas paprasta. Kiekvienas iš šešių sveikinasi su penkiais. Todėl reikia šešis padaugint iš penkių, ir padalint iš dviejų ( kitaip kiekvieną pasisveikinimą įskaitysim du kartus). Gauname penkiolika.
Na, o jei šešiasdešimt keturi žmonės, tai…
Šešiasdešimt keturi daugint iš šešiasdešimt trijų, ir dalint iš dviejų. Gauname du tūkstančius šešiolika.
Papildoma užduotis Jums:)
Kiek įstrižainių turi šešiasdešimt penkiakampis?
mokinys, 2015-04-10 17:09:38
spėju,kad šį kartą gausis 2015, o sprendžiant tuo būdu reikėtų atmesti 65 kraštines, ačiū už paaiškinimus ir uždavinukus
Sokolovas, 2015-04-10 17:23:55
Mokiniui
Šaunuolis! Aišku, reik “atskirt grūdus nuo pelų” 🙂
Ir dar. Gali praturtint savo laisvalaikį, įrodydamas štai ką:
Iškilasis n-kampis turi n(n-3)/2 įstrižainių.
Vilniete, 2015-04-10 17:43:27
Ačiū už sprendimų paaiškinimus. Įdomios užduotys. Deja, matematika nėra mano stiprioji pusė. Aš humanitarė.
qwerty, 2015-04-10 18:12:49
Aš tai net klausimo nesuprantu. Ką reiškia turi n(n-3)/2 įstrižainių? Paaiškinkite, kas galit)
Sokolovas, 2015-04-10 18:21:35
Pasiūlyta įrodyti, jog daugiakampis, turintis n kraštinių, turi n(n-3)/2 įstrižainių.
Aiškinu populiariai.
Šešiakampis. n=6. Turi 6(6-3)/2 = 9 įstrižaines ( lengva patikrinti).
Dvylikakampis. n=12. Turi 12( 12- 3)/2 = 54 įstrižaines…Ir t.t.
O jei paskaičiuosime, kiek įstrižainių turi 65-kampis, gausime 65( 65- 62)/2 = 2015.
Taigi, gyvename daugiakampio metais!
Stebėtoja, 2015-04-10 18:32:57
nieko tokio qwerty, kai čia pasimokysi matematikos n metų viskas bus aišku.:) Pasakas jau seki puikiai !!!!
O B.Burgis suklydo įvardindamas vieną žmogų priklausomą nuo interneto , dėl kitų savybių nesiginčiju. Bet jei suskaičiuoti matematiškai įmanoma, tai kokį 50 proc. jau priklausomi ir dar koks 10 proc. lipa į tą priklausomybę.:)O gal ir klystu, neskaičiavau, bet taip” rodosi”:)
Vilniete, 2015-04-10 18:48:16
Sakyčiau, pats B. B. priklausomas nuo interneto. Sprendžiu vien iš to, kokiu greičiu ištrinami jam nepatinkantys komentarai :-).
qwerty, 2015-04-10 18:56:57
Sokolovai, o kodėl visuomet -3 ir /2? Čia formulė tokia, ar kaip? Koks aš kvailas matematikoje…(
Stebėtoja, 2015-04-10 19:04:57
qwerty, tu nekvailas, tau neįdomu ir lauki Rasos.:)
Aš už.:)
qwerty, 2015-04-10 20:24:56
Aš laukiu kol Sokolovas paaiškins, nes tikrai šioje dalyje nesuprantu
Sokolovas, 2015-04-10 21:13:44
qwerty
TAIP, BŪTENT FORMULĖ ĮAMŽINA DĖSNINGUMĄ…
Paaiškinsiu jos “gimimo aplinkybes”.
Tegu daugiakampis turi n viršūnių. Iš kiekvienos viršūnės eina n-1 atkarpų. Atkarpos- tai kraštinės ir įstrižainės. Taigi, tenka daugint n(n-1). Dar reikia padalint iš 2, nes kitaip ta pati atkarpa ( pavyzdžiui- AB) bus įskaityta du kartus ( kaip AB ir BA).
Taigi, atkarpų turime n(n-1)/2.
Kad gautume įstrižainių skaičių, reikia atimti kraštinių skaičių, t.y. n atkarpų. Gauname:
n(n-1)/2 – n . Subendravardiklinę gausime
:n(n – 3)/2.
Taigi, viskas paprasta…
qwerty, 2015-04-10 22:42:38
Sokolovui, ačiū. Viskas po truputį aiškėja. Tačiau dar iš to išaiškinimo, pas mane trys klausimai atsirado. Nes trijose vietose neaišku. Bet bijau klausti, nes pasiusite mane toliau už kvailumą)
Sokolovas, 2015-04-10 22:52:39
qwerty
NA, GREIT IR NEGALI AIŠKĖTI. UŽDAVINIAI UŽ MUS VISUS STIPRESNI…
Būtinai klauskite, jei kas. Domėkitės. Be klausimų neliktų ir mokslo.
O tuo tarpu…Galite paimt rašymo priemonę, popierių, ir…brėžt įvairius daugiakampius, skaičiuot, kiek yra įstrižainių. Pradėkite nuo keturkampio. Jis turi dvi įstrižaines, penkiakampis- penkias, šešiakampis- devynias, septinkampis- keturiolika…Dar ir dar kartą susidomėsite dėsningumu ( didėja…sudėtingai…dėsningai). Tiesiog pieškite…Bus įdomu…Ir aiškės po truputį.
Sokolovas, 2015-04-10 22:54:27
PAPRASTAS UŽDAVINYS IŠ SERIJOS “ĮŽVELK DĖSNINGUMĄ”
Įžvelkite dėsningumą, ir pratęskite raidžių seką:
v, d, t, k, p, ……
Iš šalies, 2015-04-10 23:03:13
gal š, s, a, d… ?
Sokolovas, 2015-04-10 23:13:04
Teisingai!
Štai Jums pavyzdys, kai DĖSNINGUMAS YRA, jis nesunkiai įžvelgiamas, o FORMULĖS NĖRA.
Taigi, dėsningumai yra kur kas platesni už formules!
Na, ir ( prieš naktį) kitas, gal kiek sudėtingesnis pavyzdys.
Kaip pratęsti tokią skaičių seką?
1, 1, 2, 3, 5, 8, 13, 21, …..
Elin, 2015-04-10 23:23:26
Stebiuosi, iš kur tiek MATEMATIKAS Sokolovas turi ramios kantrybės šioje erdvėje su humanitarais-matematikais ?:)
Iš šalies, 2015-04-10 23:25:14
34, 55, 89, 144, 233, …
Vilniete, 2015-04-10 23:47:17
Elin, sutinku – ramios kantrybės, geranoriškumo svetainės lankytojams ir lojalumo svetainės šeimininkui. Nepaisant nieko.
Gediminas, 2015-04-11 00:05:20
Dėl tarpusavyje besisveikinančių 64 žmonių. Tai juk baigtinis skaičius junginių po 2 elementus kuriu tarpusavio išsidėstymo tvarka nesvarbi, nes nesvarbu ar Jonas spaudžia ranką Petrui ar Petras Jonui. Tai deriniai C iš 64 po 2.
Sokolovas, 2015-04-11 07:43:09
Gediminui
Taip, be abejo. Tai derinių iš 64 po 2 skaičius.
Jei, pavyzdžiui, tie 64 žmonės ne tik pasisveikintų, bet ir apsikeistų vizitinėmis kortelėmis, tai tų kortelių būtų išdalinta 64 х 63 = 4032. Tai- gretinių iš 64 po 2 skaičius ( arba elementarioji kombinatorinė daugybos taisyklė).
Bet aš aiškinau kitaip, nes daugeliui žmonių šios sąvokos yra sudėtingos…
Sokolovas, 2015-04-11 07:51:38
Iš šalies.
Taip! Tai yra vadinamoji Fibonačio seka ( Fibonačio skaičiai). Kaip matote, dėsningumas įžvelgiamas lengvai. Kiekvienas sekos narys, pradedant trečiuoju, yra lygus dviejų prieš jį buvusių narių sumai, o pirmieji du sekos nariai- vienetai.
Tačiau Fibonačio sekos n-jo nario formulė, t.y. taisyklė, leidžiantį apskaičiuoti Fibonačio sekos narį, žinant jo numerį, yra gan sudėtinga….
Temidė, 2015-04-11 11:57:59
Sokolovai, įsišėlot!?
Labai primityvūs uždavinukai: daugiakapio įstrižainės, Fibonačio skaičiai, …
O gal geriau panagrinėkit kaip Fibonačio skaičių sekoj pasiskirstę pirminiai skaičiai? Kokius dėsningumus įžvelgiat, Sokolovai?
Apie Tribonačio skaičius teko girdėt?
Temidė, 2015-04-11 12:07:50
n-ojo nario formulė nelabai sudėtinga: http://en.wikipedia.org/wiki/Fibonacci_number Aišku, aukso pjūvis atsiranda.
O kodėl, Sokolovai, seką pradedat nuo 1, o ne nuo 0?
Sokolovas, 2015-04-11 12:34:04
Temidei
Tribonačio skaičiai
T(1) =0, T(1)=1, T(2)=1.
T(n+3)=T(n) +T(n+1)+ T(n+2)
Sokolovas, 2015-04-11 12:46:23
FIBONAČIO SEKOS 1, 1, 2, 3, 5, 8,…
n-ojo NARIO FORMULĖ
Pažymėkime šaknį iš 5 raide S,
(2cos36) laipsniu n pažymėkime raide A. Kosinuso argumentas užrašytas laipsniais ( beje- 2cos36 yra įžymioji Dieviškoji proporcija, kitaip dar žinoma aukso pjūvio pavadinimu).
Tada Fibonačio sekos n-sis narys yra
F(n) = (1/S)( A + 1/A), jei n nelyginis, ir
F(n) = (1/S) ( A – 1/A), jei n lyginis.
Taip pateiktų formulių teisingumu lengva įsitikint paprastu skaičiuokliu.
aina na, 2015-04-11 14:18:39
UžDAVINYS; Žodžiais pratęskite skaičių seką:
1,2,3,4……………………….
Trakimas, 2015-04-11 23:49:10
Aritmetiku rungtynes:)Juokinga iki asaru—
Trakimas, 2015-04-12 00:27:19
Maniau ,kad Sokolovas ims i paaiskins apie trimates plokstumas ir dvimates erdves?O jis tce aiskina apie kiekybinius “ranku paspaudimus” ,kurie galu gale atneshtu naudos otkatu pavidalu:)Taisykle,kad 1+ 1 =2 nera Sokolovo demesio centre.Jis muset nori irodyti,kad paspaudus ranka 2000 savivaldybes klerku,1+1 bus jau lygu 64?:)
Sokolovas, 2015-04-12 12:18:39
KAM REIKALINGAS “PRIVALOMAS MATEMATIKOS EGZAMINAS”?
Aišku, aš būčiau tik UŽ. Už išties privalomą matematikos egzaminą, koks buvo prieš daugelį metų. Kaip ir už tokį matematikos dėstymą, koks buvo tada, kai aš pats mokiausi…Algebra, geometrija, privalomas įrodymų mokėjimas, žodinės apklausos ( ugdžiusios gebėjimą reikšt mintis…). Ir…Egzaminai. Privalomi. Baigiamieji bei stojamieji. Ir…net paskutinis dvejetukininkas mokėjo (a+b)kvadratu…Dabar net studentui tai būna problema…
Tuo tarpu dabar vėl planuojamas “privalomas” matematikos egzaminas. Tai gal…Gal pripažinta, jog būta klaidų, ir imtasi taisyti padėtį?
Nieko panašaus!
Visų pirma- pati nuostata, esą jis bus “privalomas” tik “kažko norintiems” ( valstybės finansuojamų studijų, ar pan.) paneigia pačią “privalumo” sampratą. Privaloma yra tai, kas privaloma norintiems gaut atestatą, o ne “baltą bilietą”. Bet apie tai nekalbama. To kratomasi.
Dėl nemokamų studijų. Aukštosios mokyklos ir dabar gali nepriimti tų, kas nelaikė dabartinio valstybinio matematikos egzamino. Bet to nėra!
Taigi, “privalomas” matematikos egzaminas bus tik vaidyba. Ir gan pavojinga vaidyba. Jo įvedimas griaus tai, kas (dar) yra- dabartinį matematikos egzaminą. Jis bus pasityčiojimas iš matematikos, kokiu jau tapo dabartinis “privalomas” dešimtokų matematikos žinių patikrinimas ( nuo trupmenų sudėties iki laužavietės ploto skaičiavimo “kuoliukais”). Ne be trūkumų yra dabartinis valstybinis matematikos egzaminas, bet…vis dėlto ten dar lieka grynos, “buitinio pragmatizmo nesugadintos”, matematikos.
Matyt, siekiama griauti toliau…
Sakiau ir sakysiu- “vanagai-reformatoriai” geriausiai “daro” tik tada, kai nedaro nieko. O jei ką pradeda, tai…ir apokalipsės perspektyva neatrodo tokia baisi…
Atsakymas, 2015-04-12 14:21:39
Sokolovui: http://www.mundusinversus.com/varia/humanitarai-numarino-matematika-tesiilsi-ji
Trakimas, 2015-04-12 20:17:24
Aš kategoriškai prieš privalomą matematikos egzaminą.Nes privalomas “egzaminas” atrinks tik tokius pačius “sokolovus”,kurie rengs užduotis:)Visus gabius “perelmanus” tokie “egzaminai” atsijos iš anksto.
Trakimas, 2015-04-12 20:20:58
Kas yra “egzaminas”?Egzaminas yra siena,kuri tam ir pastatyta,kad neleistu jos įveikti inovatyviems jaunuoliams ir jų konceptams.Egzaminas yra “atvirutė iš praeities”,kaip taikliai apibūdino Derrida.:)
Sokolovas, 2015-04-12 20:43:59
UŽDAVINIŲ KOLEKCIJA
Tokias kolekcijas duodu mokiniams…
- Laivo greitis, plaukiant upe pasroviui, lygus 12 km/h, prieš srovę- 8 km/h.
Raskite A, t.y. upės tėkmės greitį
- Tam tikrą kelią upe pasroviui laivas nuplaukia per 8 valandas, tą patį kelią prieš srovę- per 12 valandų.
Per kokį laiką šis laivas nuplauktų tą patį kelią stovinčiame vandenyje? Atsakymą išreikškite valandomis, ir pažymėkite B.
- Stačiakampio įstrižainės ilgis 20, kampo tarp įstrižainių didumas 30 laipsnių.
Apskaičiuokite S, t.y šio stačiakampio plotą.
- Trikampės piramidės visos keturios sienos- statieji trikampiai. Ilgiausios briaunos ilgis yra 12.
Apskaičiuokite R, t.y. apie šią piramidę apibrėžtos sferos spindulį.
Ir…Lemtinga akimirka!
Apskaičiuokite
2BS + 8AR – 1
P.S. Uždavinių kolekcija nauja, ir labai lengva. Prieinama bene kiekvienam. Pabaigoj tampa itin įdomu…
Trakimas, 2015-04-12 21:02:31
“Upes tekmes greiti” kurioje koordinaciu sistemoje?sokolovai?Uzduotis nera ishbaigta.Jus nutylite tai,kas Jumim savanaudishkai atrodo savaime suprantama.Taciau matematikoje nieko nera “savaime suprantamoi” .Jus tiesiog klaidinate respondentusmbandydamnaS juos itraukti isava interesu zona–
Rasa, 2015-04-12 21:08:42
O vargeli, kaip miela!!! Sokolovai! Šitas uždavinys su upe, kažkada, kai buvau pradinėse klasėse, iškėlė man pirmą labai labai svarbų man gyvenime klausimą. Kuo skiriasi supratimas nuo suvokimo 🙂 Niekad gyvenime nepamiršiu. Jau prieš mokyklą gana gerai galėjau sudėti, atimti, dauginti ir dalinti, ir puikiai supratau vieną formulę dar: s lygu v padauginta iš t 🙂 Čia man viskas derėjo- kelias, laikas ir greitis buvo suprantama. Ir jų tarpusavio ryšys toje formulėje. Tačiau paskui, kai ėmiau lankyti mokyklą, mokytoja uždavė va tokį uždavinį su laivu! Niekas dėl to nesuko galvos- na pridedame upės greitį ar atimame. O aš ėjau ir visų klausinėjau- KODĖL?! Aš mokėjau teisingai išspręsti uždavimį, t.y. supratau, nes taip reikia. Tipo. Bet aš nesuvokiau kodėl. Juk laivas plaukia sau, o upė sau. Kaip galima upę pridėti prie laivo? Juk nedera jie ir viskas. Upė sau. Laivas plaukia sau. Savo greičiu. Visi bandė man paaiškinti. Ir visi iš manęs juokėsi. Tada aš nebenorėjau atrodyti kvaila, nutilau ir tiesiog teisingai sprendžiau. Pridėjau upę ir atiminėjau. Kaip reikia… Kaip visi… 🙁 Bet mintyse buvo liūdna, nes upė nelimpa prie laivo…
Ir koks palengvėjimas man atėjo po kelerių metų, kai per vieną pirmųjų fizikos pamokų aš pagaliau suvokiau esmę. Nes buvo tokia pamoka apie žmogų vagone. Ir aiškinomės jo judėjimą. Kas gaunasi, jei vagonas stovi, važiuoja, važiuoja į kitą pusę. Jei žmogus vagone stovi, eina į vieną pusę ar į kitą… 🙂 Kaip keičiasi jo judėjimas žemės, vagono atžvilgiu ir t.t. Ir tada pagaliau sau supratau, kad fizika- tikras stebuklų mokslas ir jei ją suprasi, tai visokių neregėtų negirdėtų stebuklų ir jų paaiškinimų sužinosi :))))))
Sokolovas, 2015-04-12 21:09:26
Trakimui
Tai iš serijos “į siūlių tūrį neatsižvelkite” , kai prašoma apskaičiuoti palapinės tūrį? 🙂
Žinote, va per tokius “akademikus” uždavinių tekstai kartais tampa ilgi bei mokiniams nesuprantami.
Žinote, tokiais atvejais gal kas nors pasakytų-“neapsimeskit šlangu” 🙂
Aš taip nesakysiu. Tiesiog siūlau- spręskite Kolekciją, gerb. Trakimai! 🙂
Trakimas, 2015-04-12 21:14:26
Meluojate ,sokolovai.Tai nera “siuliu turio” nuokrypos.Mes nesutinkame del esmes.
Trakimas, 2015-04-12 21:23:14
Uzdavinio salyga:
Kuo skiriasi odontologas nuo kardiochirurgo?Jie abu yra medikai.
Sokolovas, 2015-04-12 21:28:19
SUPRATIMAS ATSILIEKA NUO VYKDYMO…
Rasai
O žinote, juk tai nuostabu !
Apie tai nerašo deklaracijose, nes tai nepatraukliai skamba…Bet…Kiek tikrovėje yra dalykų, kurie yra nutylimi vien dėl to, kad yra nepatogūs. Ir tiesa tuomet trečiajam plane lieka.
O kaip gražiai skelbiama “deklaracijose”, esą “reikia suprast, reikia tik suprasti…” Gražus, į blizgantį aukso popierėlį įvyniotas melas!
Neneigiu- suprast reikia! Būtina! Bet tai yra ilgai siekiamas, GALINIS ( o ne pradinis) mokymo vyksmo tikslas! Tiesa ( ta, apie kurią visi tyli) yra gan žiauri- supratimas atsilieka nuo vykdymo!
Iš pradžių mokinys “vykdo” ( valio kantrybei bei darbštumui!), ir tik ilgainiui ateina supratimas…
Va ir Jums taip buvo. Iš pradžių vykdėt, įpratot, “susidraugavot su formule”, o tik vėliau atėjo supratimas.
Turbūt prisimenate tokį “paukštį” kaip diskriminantas. Ir dabar daugelis mokinių moka jo formulę, moka jį apskaičiuoti. Bet…Net mokslo pirmūnai Jums nepasakys, pavyzdžiui, kodėl ten yra minuso, o ne pliuso ženklas! Štai ir čia- vykdo, bet nesupranta. Ir tik nedaugelis, ir tik vėliau pasidomės tuo, kaip “gimsta šis paukštis”, ir džiaugsis supratęs tą paslaptį…Aišku, pavėluotai…Aišku, nedaugelis…Džiaukimės supratimo akimirka, neliūdėkim dėl “vykdymo metų” tėkmės…
Tokia jau mokymosi vyksmo upės tėkmė- supratimas nuo vykdymo atsilieka. Nes sąmonė atsilieka nuo būties.
Rasa, 2015-04-12 22:35:51
Ne visai tas pat, kai vykdai, įpranti, o paskui supranti. Suvokimui būtina tai, kai suvoki esmę. Supranti, tai būna tada, kai supranti- žinai. Žinai faktus, dėsningumus, sudėtį ar dar ką nors. O suvoki kažką, kai dar ir suvoki- gal tiktų apibūdinimas, kad pajauti? Suvokti- tai turbūt suprasti sąmoningai. Ne todėl, kad įpranti ir išmoksti, o todėl, kad suvoki pačią esmę savimi. Tarkim matematikoje tai tada, kai tu įrodai teoremą, o ne tada kai sėkmingai taikai formules. Tada, kai moki formulių nedaug, bet tu suvoki jas ir žaidi jomis, statai iš jų, išvedi kitas, gėriesi jomis… Po teisybei man tai jau beveik pamiršta, aš labai seniai atsisveikinau su tikrąja matematika 🙂 Nors, kai dukra kažko nesuprasdavo, o aš jau buvau pamiršus viską, kartais mes mokydavomės abi labai juokingai- ji man išdėstydavo taip, kaip dėstė mokytoja, o aš paskui jai atgal išdėstydavau kitais žodžiais ir abiems pasidarydavo aiškiau 🙂
Deja ir kasdieniam gyvenime susiduriam su tuo pačiu. Kaip daug žmonių visko žino, kaip mažai išties daug suvokia… Žinios dabar lengvai prieinamos. Bet žinios yra tik “formulės”, o esmė yra visuomet giliau. Net jei meilę paimtume 🙂 Juk pavasaris! 🙂 Kiek daug žmonės kalba apie ją, žino- nuo meilės chemijos, fizikos, psichologijos, poezijos, romantikos ir ko tik nori. O kiek žmonių moka išties mylėti? Sąmoningai. Nesavanaudiškai. Giliai. Švariai. Mažai moka. Man taip atrodo. Ir ko vertos visos žinios apie meilę, jei niekada nesi mylėjęs? 🙂 O jei ir esi mylėjęs, tai su metais pamatai, koks menkas meilės atspindys buvo tai, kas tau atrodė visa ji. Taip ir su matematika, su viskuo. Suvoki- tai kai tu suvoki uždavinį, kai žaidi, draugauji, o kartais kauniesi su juo, kai sukioji ir vartai jį, kai pyksti ir vėl susitaikai. Aš taip seniau spręsdavau. Dabar nebemoku 🙂 Visuomet matematiką (sunkiausius uždavinius) pasilikdavau paskutinius ruošti. Ir tada visą laiką skirdavau jiems, žaisdama- kuris nugalėsim? Aš jį ar jis mane? Ir kaip smagu, kai eidavau miegot kaip nugalėtoja! 🙂 Tai liečia visus mokslus, kuriuose buvo reikalingi skaičiavimai- žaidimai. Bet iš visų jų jau pamenu tik tą gerą jausmą, nes pamiršau jau visus, kuriuos mokiausi- techninę mechaniką ir šilumines technologijas, elektrotechniką, fiziką. Visur reikėjo dėlioti- skaičius ir įrenginius, varžas ir detales- buvo labai smagu… Mokytis- tai nuostabu!!! Ne “kalti” pažymiui, o būtent mokytis- suvokti tai, ką mokaisi. Sunku, bet nuostabu.
qwerty, 2015-04-12 23:21:06
Sąmoningai mylėti…hmm. Gal, ir galima, nežinau.Nesuvokiu.Nesuprantu. Tačiau žinau, kad stipriausia, tikriausia meilė yra tuomet, kai myli instinktyviai.
Rasa, 2015-04-12 23:44:31
Qwerčiui: nesiginčysiu 🙂 Gal. Nebent truputį. Nes juk aš nežinau, kas tau yra Meilė. Štai šiandien kai ką paskaičiau: “Vis nešiojasi Viliaus Orvido palikti žodžiai apie žodžius: „Žodžiai, kuomet juos pasakai, labai bejėgiai palieka“.” Tai štai aš ir manau, kad daugeliui dalykų apibūdinti kartais žodžių nepakanka 🙂 Nevienodai mes žodžius suprantame. Dažnai.
Paimkime tavo “instinktyviai”. Štai turime čia tokį jaunuolį moterišku vardu- Temidę. Su gerai veikiančiu vienu “instinktu”. Pamato jis jauną panelę ir supranta- instinktas sako: man ji patinka, nes jos noriu! Laaaaabai noriu!!! Jei labai noriu turėti, tada myliu ko gero 🙂 Ir ima siekti apsiblaususiomis akimis tos norimos… Paskui “instinktas” kažko sumažėja, žiūri ir nelabai jau nori… O galvojo, kad čia meilė, kad čia ilgam… Juokauju, žinoma, Temidės atsiprašau iš anksto. Jis gali laikyti kad tai mano atsakas į jo susirūpinimą mano seksualiniu gyvenimu, apie kurį svarstė senesnėje temoje 🙂 Ir man dar anaiptol nėra 50-ies, jeigu ką (čia irgi jam :). Tai va, o kai meilė ne vien instinktas (man instinktas daugiau panašu į aistrą ar pirminį potraukį), tada viskas būna šiek tiek kitaip. Man taip atrodo. Šiaip jau sąmoningai mylėti, reiškia ne tik kažką jausti, bet ir suvokti savo jausmus- kokie jie išties. Tai ne tik malonumo siekimas, ne tik noras turėti, ne tik rožinės svajonės- tai daugiau. Tai kai laimėje ir varge… 🙂 Gal būt esu neteisi. Daug su kuo pasikalbam apie meilę ir žmonės pyksta, kai kartais aš parodau jų vienokį ar kitokį jausmą, jų vadinamą meile, jiems šiek tiek kitu kampu 😉 Aš pritarčiau tau, kad įsimylima instinktyviai, o paskui tai ne visada perauga į meilę (jei imtume priešingos lyties žmonių tarpusavio meilę, o ne meilę apskritai 🙂
skaitovas, 2015-04-13 08:30:04
Sakalauskai, nenurimsiu – „vanagai-reformatoriai“?
Sokolovas, 2015-04-13 09:05:09
“PAGAL JŲ DARBUS…”
Skaitovui
Matote, va toks paradoksas su manim- moku parodyt, kur yra musė, bet nemoku parodyti, kur yra dramblys.
Nes…Visada būna sunkiausia paaiškini akivaizdžiausius dalykus.
Kaip ir matematikoje. Pavyzdžiui, visi žino, kas yra taškas, kas yra tiesė, kas yra plokštuma…Bet atitinkamų apibrėžimų nėra!
Arba…Sakau mokiniui- pažymėk tašką, simetrišką duotajam šios tiesės atžvilgiu. Dauguma pažymi. Nes tai ne tiek matematika, kiek pasaulėjauta! Kai kas “nesupranta”. O su tokiais- sunkiausia! Nes būta dalykų, kurių “išaiškinimas” būna daug sudėtingesnis už pačius dalykus…
Tas pats ir su tais “vanagais”.
Ką aš galiu “išaiškint”? Pavardes, pareigas? Nei man, nei kitiems jie “neprisistato”, nes mes jiems nereikalingi, mes jiems tik kliūtis. Tačiau…
Pagal jų darbus jie yra matomi!
Kas bene kiekvieną “penkmetį” keičia mokymo programas, neva atsižvelgdami į kažkokią, tik jų vaizduotėje gyvuojančią, “bendruomenę”? Nors pagal ankstesnę programą jau yra išleistų vadovėlių, tam yra išleista nemažai valstybės pinigų…Ne, jiems netinka- praeina keleri metai, ir vėl “kitaip reikia” ( šiaip tai čia akivaizdus valstybės lėšų švaistymas, o kur dar švietimo sistemos klibinimas ! ).
Arba- “išsižiojusiai” iš nuostabos “bendruomenei” pranešama, jog “pagal bendruomenės pageidavimus mokslo metai tęsis ir birželį”. Sakykite, kaip Jūs įvardintumėt asmenis, kurie nukreipia savo ( nežinią kokiu pagrindu kildintą) “galią” tam, kad sukurtų jūsų “pageidavimus” ir “vykdytų juos”? Gal tikrai, apibūdinimas “vanagai” čia netinka? Nes…Kuo čia dėti paukščiai? Bet, kaip kadaise tarė Pontijus Pilotas- “kaip pavadinau, taip pavadinau”…
Taigi,- sunkiausia yra apibrėžt akivaizdžiausius dalykus. Tačiau PAGAL JŲ DARBUS MATOMI JIE! Tie, kas “rūpinasi mumis” vien tam, kad legitimizuotų savo uždarbius bei abejotinai-legitimias “pareigas”.
Išsišokėliai primena vanagus? Ar baltuosius balandžius? Epitetų laisvė- irgi demokratija…
petras, 2015-04-13 10:07:42
demokratija nėra laisvės priežastis
skaitovas, 2015-04-13 12:00:58
Sokolovui: ačiū už tokį ilgą ir nuoširdų atsakymą!
Taip, surašėte tuos dalykus, kurie tarsi akivaizdūs. Daug visokių sąmokslo teorijų – tikrų ir nelabai – yra prikurta apie tai, kodėl vyksta visokios pertvarkos švietime. Svarbiausia – kodėl. Priežasčių viešoje erdvėje ir neoficialiuose pokalbiuose yra n+k+1 (jei aš teisingai juokelius iš matematikos mokyklinio kurso atsimenu). Iš tiesų, vieni reformuoja, t.y. griauna ir ant griuvėsių stato iš anksto renovuotinus objektus todėl, kad taip liepia jų komjaunuoliška prigimtis. Kiti – todėl, kad yra absoliučiai nekompetentingi, bet nori parodyti savo aktyvumą. Treti – tik pragmatišką norą nukreipti visuomenės dėmesį nuo svarbesnių problemų. Ketvirti – …
Ką aš tuo noriu pasakyti? Na, netinka visiems švietimo pertvarkų vadovams vienas ir tas pats terminas, kurį Jūs siūlote. Nėra vieno dėsningumo, dėsnio, teoremos, aksiomos. Kaita Lietuvos švietime nėra matematika. Aš jai aiškinti labiau siūlyčiau taikyti istorijos modelį, kuriame greta bendrų priežasčių dažnai veikia įvairūs asmeniniai faktoriai. O jie dažniausiai perspjauna, nulemia bendrus raidos dėsningumus. Tad visų pertvarkų iniciatorių „subendravardiklinti“ mano galva nederėtų.
Juo labiau, kai kalbame apie KTUG atvejį. Nepatikėsiu, kad KTUG įvykiai – ŠMM noras paversti ją eiline beveide gimnazija. Priežastis? Net ir tie veikėjai supranta, kad Lietuvai reikia gabiųjų vaikų peryklų. Reikia medalių tarptautinėse olimpiadose. KTUG ilgai buvo tokia perykla (gerąja prasme). Bet… Paanalizuokit visų VBE rezultatus nuo kokių 2011 metų ir pamatysit, kad pati KTUG pradėjo tolti nuo Vilniaus Licėjaus ir artėti prie pilkųjų gimnazijų masės. Jei ką, paklauskit Jūsų proteguotos kandidatės V.D. – ji suskaičiavo. (Mano kolega gavo šiuos skaičiavimus konkurso posėdyje).
Išvada: mano akimis, reformos lizdas šiuo konkrečiu atveju ne A. Volano gatvėje. Gal reikėtų ieškoti arčiau gimnazijos?
Random, 2015-04-13 18:21:02
Skaitove, o jūs ar žinot kaip reitinguojamos mokyklos pagal egzaminus? Šimtukų skaičiumi, o ne procentu… Licėjuj daugiau nei dvigubai mokosi, bet KTUG net ir skaičiumi nelabai atsilieka, o anglų egzamino šimtukais net lenkė, bent 2013 metais 🙂
skaitovas, 2015-04-13 20:43:59
Random: as nesigilinau, bet manau, kad pretendente V.D. neturejo tikslo nesuprasti elementarios matematikos. Beje, net ir as visa laika matau procentus, bet ne absoliucius skacius. Tiesa, ne apie tai kalba…
Temidė, 2015-04-13 22:32:51
Matematika – juk ne seksas! Kam ja užsiiminėt kasdien?
miklis, 2015-04-13 22:58:26
Lygiai tam pačiam, kam užsiminėti meninkui kasdieną menu. Kad priartėtų.
Rasa, 2015-04-13 23:09:56
Prieš miegą kažkodėl užsigalvojau- instinktas ar intuicija? Kuo jie skiriasi? Į kurį iš jų reikėtų daugiau įsiklausyti? 🙂
qwerty, 2015-04-13 23:29:38
Rasa, savo vaikus, mamą, kaip myli?
Rasa, 2015-04-14 08:37:53
Qwerčiui: Meilė vaikams pas mamas dažniausiai prasideda kaip instinktyvi. Bet ir tai ne pas visas vienodu metu. Šiek tiek mitas, kad vaikutis gimsta ir staiga mamą užplūsta begalinė meilė… Ne pas visas tai būna.
O meilė tėvams… Jei manytume, kad tai instinktas, tai stebint visą gamtą matytume, kad suaugus vaikai palieka tėvus, nes jie tampa “našta”, o instinktai reikalauja tęsti savą giminę. Pas žmones tai kartais pasireiškia sunkiau, nes paaugliams ima veikti tas instinktas, o realiai jie dar negali palikti namų, jie būna dar labai priklausomi nuo tėvų- materialiai, teritoriškai, dvasiškai ir juridiškai. Iš to ir kyla tos didelės problemos su paaugliais, kai tėvai verčia vaikus paklusti ir būti vaikais, o vaikams reikia eiti pirmyn. Paskui, po kelerių metų, santykiai paprastai susitvarko 🙂 Bet suaugusiam mylėti tėvus- jau nėra instinktas 🙂
Man taip atrodo.