Net jei nemėgstate matematikos, vis tiek perskaitykite!
*
Vakar atėjo du gimnazistai ir paprašė padėti išspręsti tokį uždavinį.
Duota viena trikampio kraštinė ir to trikampio aukštinė. Kokio didžiausio ploto stačiakampį galima įbrėžti į tą trikampį?
*
Aš nemėgstu geometrijos (nes pamiršau; nes nemoku braižyti; nes mano geometrinis matymas silpnas…), bet mėgstu išvestines, ekstremumus.
Iškart supratau, kad gimnazistai atsinešė sunkų uždavinį, nes neapibrėžtą: kuri aukštinė duota – į duotąją kraštinę ar ne? kur įbrėžiamas stačiakampis – prie duotosios kraštinės ar ne? Susidaro daug variantų, iš kurių vieno visai nemoku išspręsti, niekada nemokėjau, todėl čia ir rašau jums…
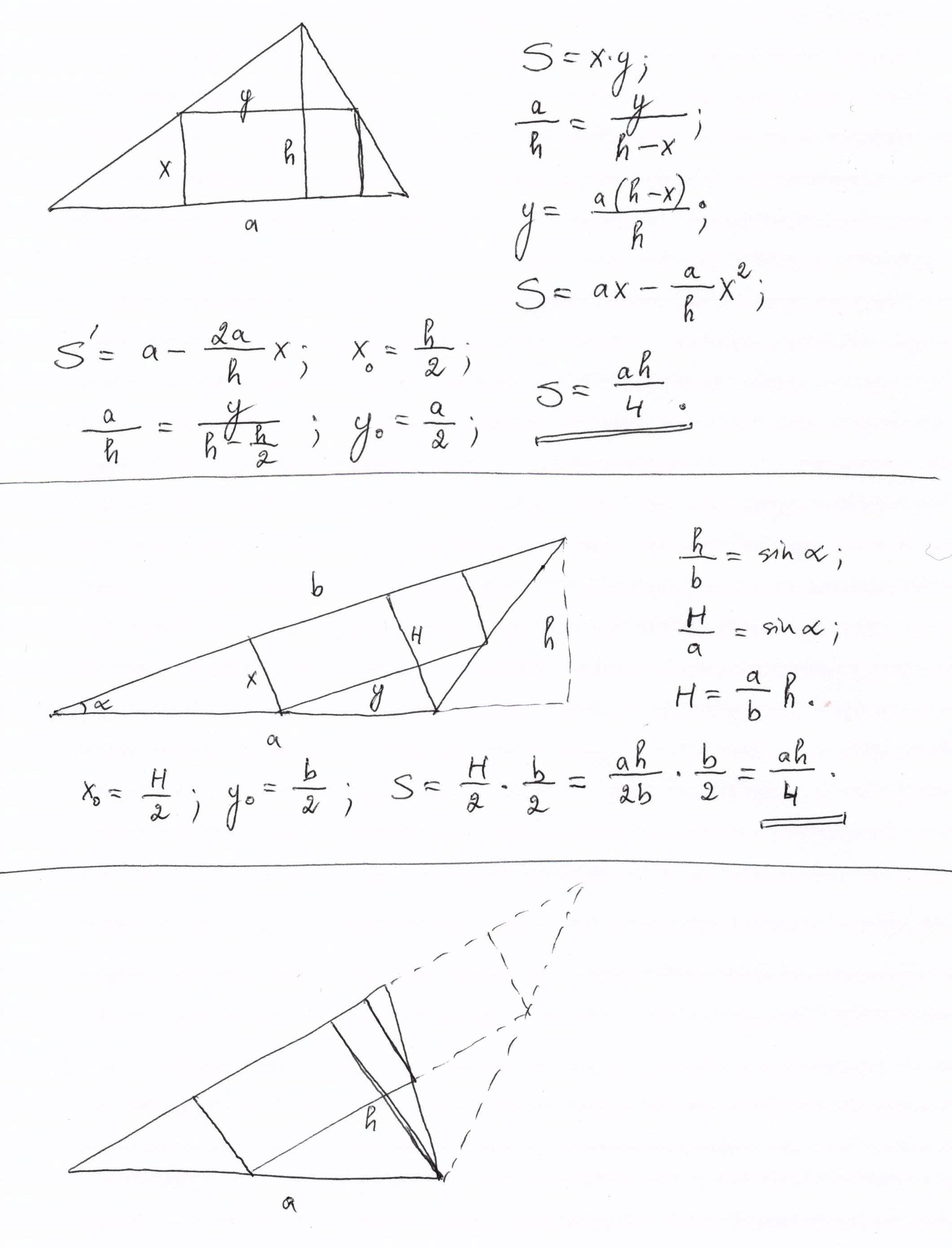
Pradėkime nuo aiškiausio varianto – aukštinė į duotąją kraštinę, o stačiakampis priglaustas prie duotosios kraštinės. Sprendimą randame greitai (žr. pav.), atsakymas įdomus net nemėgstantiems matematikos!
*
Antras variantas – aukštinė į duotąją kraštinę, bet stačiakampis glaudžiamas ne prie duotosios kraštinės. Šįryt radau, mano supratimu, įdomų sprendimo debiutą. Atsakymas (žr. antrąjį pav.) jus turėtų sudominti!
*
Trečiasis variantas, kai aukštinė ne į duotąją kraštinę (žr. trečiąjį pav.), vienareikšmiai neišsprendžiamas. Bet gal aš klystu?
*
O filosofiškai įdomiausias klausimas, į kurį nemoku rasti atsakymo ne tik šiame uždavinyje, yra toks: kaip įrodyti, kad didžiausio ploto stačiakampis būtinai bus tas, kuris vienu šonu priglaustas prie kurios nors kraštinės? O gal galima rasti didesnio ploto stačiakampį, kuris tiesiog kažkaip „kreivai įdėtas“ į trikampį? Gal koks nors stalius, norėdamas iš trikampio formos plokštės išpjauti didelį stačiakampį, rastų tokį sprendimą? Intuicija sako, kad nerastų, bet kas ta intuicija? Reikėtų įrodyti! Nemoku. Padėkite…
Atsakymai
Burgis, 2013-01-22 09:21:40
Reitingams…
Jonas Kiselis, 2013-01-22 11:13:07
Atsimenu, ekonomikos bakalauro studijose irgi būdavo tokie uždaviniai, kaip suskaičiuoti, kokiai kainai esant monopolisto pelnas bus didžiausias (didžiausias stačiakampio plotas grafike), turint duotą paklausos funkciją (trikampio kraštinę).
Jonas Kiselis, 2013-01-22 11:25:50
Sunku komentaro laukelyje parašyti sprendimą, tačiau galiu šiek tiek sufleruoti:
Sakykime, kad kairysis trikampio kampas yra A, susikirtimas tarp a ir h yra B, o dešinysis kampas yra C. Tuomet apatiniai stačiakampio kampai turės būti atitinkamai: dešinysis vidurio taške tarp A ir B, o kairysis vidurio taške tarp B ir C.
Burgis, 2013-01-22 11:42:37
Jonui Kiseliui: tai čia pirmajam variantui? Su juo viskas aišku…
Jonas Kiselis, 2013-01-22 12:03:23
O ką trečiajame variante reikia rasti? Tą stačiakampį su punktyrine linija? Nelabai aiški sąlyga.
Burgis, 2013-01-22 12:18:07
Jonai, perskaitykite dar kartą…
Jonas Kiselis, 2013-01-22 12:28:12
Mano manymu, tik pagal duotus duomenis išspręsti neįmanoma. Turi būti dar žinoma, koks bukasis arba dešinysis kampas, arba kurios nors punktyrinės linijos ilgis.
Burgis, 2013-01-22 12:37:32
Jonui: tai ir sakau…
miklis, 2013-01-23 02:55:31
Trečiam variante pavyzdžiui gali būti aukštinė, sutampanti su kraštine.
Na, o tas filosofinis uždavinys pasirodo turi vieną labai lengvai suvokiamą sprendimą, kuriam net algebros nereikia. Palikim stačiakampio plotą fiksuotą ir ieškokim trikampio su didžiausiu plotu, tokio kad vienas iš stačiakampio kampų yra ne ant trikampio kraštinių. Be to, nė viena trikampio kraštinė nesutampa su stačiakampio kraštine. Tarkim, tokį trikampį pavyko surasti. Fiksuokim dvi trikampio kraštines einančias per ,,laisvą” jo viršūnę, o likusiąją palikim suktis apie jai priklausančią stačiakampio viršūnę (čia ,,laisva” – turėjau minty viršūnę, tokią, kad stačiakampio kraštinėms lygiagrečios tiesės jo nekirs). Matom, kad taip sukant kraštinę, didžiausias trikampio plotas ir bus tada, kai ta kraštinė sutaps su stačiakampio kraštine! Na, o kodėl taip yra, galiu palikti pagalvoti…
Dėkui už tokį gražų uždavinį 🙂
Burgis, 2013-01-24 09:18:39
mikliui: atsakymas – kitoje temoje…