Universitetuose artėja naujas semestras. Gimnazistai jau pradėjo antrąjį pusmetį. Užeinu pas trečiokus – sprendžia tokį uždavinį. Kodėl ir jums nepasprendus? O tai tik pralekiate per šią svetainę, paveikslėlius pasižiūrite ir … vėl užsiimate niekais, pavyzdžiui, verslu… :-).
Uždavinys toks:
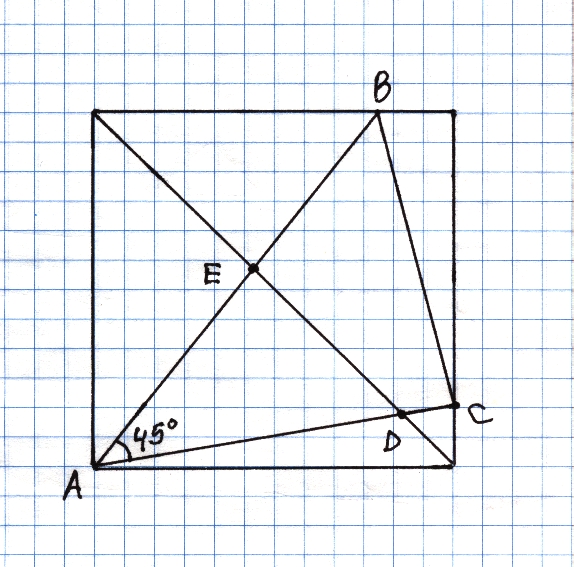
Iš kvadrato kampo nubrėžtas 45 laipsnių kampas. Įrodykite, kad trikampio ABC plotas dvigubai didesnis nei trikampio AED.
Atkreipkite dėmesį, kad jei taškas B “pataiko” į priešingą nuo A kampą, tai įrodymas trivialus (akivaizdus).
Dar viena pastaba: aš, matyt, neturiu “geometrinio matymo”, nes iš pradžių man atrodė, kad kampą brėžiant taip, jog BC būtų lygiagreti ED, taškai B ir C “pataikys” į kraštinių vidurio taškus. Ot, ir ne! Tik apskaičiavęs tai pamačiau…
Atsakymai
susimąstes, 2010-02-02 11:15:54
O tą 45 laipsnių kampą bet kaip galima sukinėt ir vistiek ta pati lygybė gautusi?
Burgis, 2010-02-02 11:37:52
Susimąsčiusiam: taip, tai ir yra esmė, kad sukiojant kampą plotų santykis išlieka 2:1
E.B., 2010-02-02 11:48:13
Na aš taip manau:
Galima trikampį ABC pasukti taip, kad liktų tik du kampai po 45 laipsnius arba kraštinę AC “paguldyti” ant kvadrato kraštinės.
Tada AC = AD. O B taškas atsirems į kvadrato tašką priešingoje pusėje nei taškas A, nes kampas 45 laipsniai.
O taškas E susidurs lygiai per vidurį. Vadinas AED plotas bus pusę ABC.
Na kažkas tokio…
Rasa, 2010-02-02 13:28:21
Labai puikus uždavinys… Pažiūrėti… :)))))))))
Aš tai eisiu geriau į darbą ir pasistengsiu ten ranka gražiai rašyti… 😛
Burgis, 2010-02-02 13:42:05
E.B.: jau rašiau, kad pasukus įrodyti nėra jokių problemų, bet kaipo įrodyti nepasukus? Arba reikia įrodyti, kad sukant plotų santykis nekinta…
petras, 2010-02-02 13:57:14
Aš tai truputi nesupratau šito uždavinio. kadangi nėra tikslių ilgių duota, tarp taškų. tai realiai aš ir galiu tą kampą padaryt, taip, kad taškas B būtų priešingam nuo taško A kampe + galim pasukt kampą taip, kad c taškas būtų priešningam kampe nei A, tai jau du kartus pavyksta gaut reikiamą plotą, o tada jau trivialu, kaip sakėt.
O jei reik įrodinėt, faktiškai šitam atvejui, kaip, kad pabrėžta, tai liniuotės reik tada man :DD
petras, 2010-02-02 13:59:55
tada jau reik sinusus visokius į pagalbą kviestis, per sudėtinga…
susimąstes, 2010-02-02 14:49:28
Manau galima tą 45 laipsnių kampą pasukt taip, kad kvadrato įstrižainė jį dalintų per pus. Tada išeina apskaičiuot susidariusių trikampių kampus ir tuo pačiu plotą. Manau, jog atitinkamų trikampių plotai būtų tokie kaip sakėt. Plius E.B. skaičiavimas ir gaunam šiokį tokį įrodymą.
Burgis, 2010-02-02 14:59:10
Ne, mielieji, ne! Sukioti negalima, tai atskiri atvejai!
Povilas, 2010-02-02 16:14:35
Nesu euklidinės prigimties, tad tokie uždaviniai man nepasitaiko, bet pabandysiu. Bet štai vienas aštuntokas man pateikė tokią užduotį: 16-koje kvadratų (4X4) išdėstyti skaičius nuo 1 iki 16 taip, kad išdėstytų skaičių suma horizontaliose ir vertikaliose eilutėse bei abiejose įstrižainėse būtų po 34. Įsitikinau, kad mano galva jau aptriušusi: užtrukau visą dieną.
Toli, 2010-02-02 16:22:07
nepažymėta, bet pasitikslinsiu: kampas ACB status? ar čia uždavinys, kad net ir bet kokiam ACB kampo dydžiui tinkamas?
Burgis, 2010-02-02 16:29:08
Apie ACB nieko nežinoma… Akivaizdu, kad bendruoju atveju jis tikrai nėra statusis (imkite simetrinį atvejį…).
matematikas, 2010-02-02 17:59:42
gal reiketu gabaleli kvadrato atkirpti ir prideti prie kito kvadrato galo ir tada pagal panasius trikampius pabaigti sprendima 🙂
GL, 2010-02-02 18:49:20
OK… as niekada nemegau geometriniu uzdaviniu (ar bent jau geometriniu ju sprendimu budu).
Taigi algebrinis 🙂
x – atstumas nuo D iki apatines krastines
y – atstumas nuo E iki kaires krastines
a – kampas i desine nuo EAD
45-a – kampas i kaire nuo EAD
Skaiciuojam ne paciu trikampiu plotus, o juos ribojanciu. Jei tie bus lygus, tai ir sitie.
x = (1-x)tan(a)
y = (1-y)tan(45-a)
tan(45-a) = (1-tan(a))/(1+tan(a))
x = tan(a)/(1+tan(a)) = 1-1/(1+tan(a))
y = 1-1/(1+(1-tan(a))/(1+tan(a))) = 1-(1+tan(a))/2 = 0.5(1-tan(a))
Visur naudoju standartine trikampiu ploto formule…
S(bottomleft) = 0.5x + 0.5y
S(topright) – S(bottomleft) = 0.5tan(a) + 0.5tan(45-a) + 0.5(1-tan(a))(1-tan(45-a)) – 2S(bottomleft) = 0.5(1+tan(a)tan(45-a) – 2(x+y)) =
=0.5(1 + tan(a)(1-tan(a))/(1+tan(a)) – 2(tan(a)/(1+tan(a))+0.5(1-tan(a))) = 0.5/(1+tan(a)) * (1+tan(a)+tan(a)-tan^2(a)-2tan(a)-(1-tan^2(a))) = 0
Negrazu, bet tikiuosi suprantama ir teisinga 🙂
GL, 2010-02-02 18:55:11
O, pamirsau pamineti, kad kvadrato krastines ilgis – 1
matematikas, 2010-02-02 20:41:17
Gal galima taip?
http://picasaweb.google.com/matematikas/BurgisForumas#5433713626833876530
mathematitian, 2010-02-02 21:11:08
Galima per panašiuosius trikampius įrodyt pastebėjus, kad <FAB=<QAC , kur F-viršutinis kvadrato kairys kampas, o Q-dešinys.
burgis, 2010-02-02 21:14:20
GL: Gediminai, kam gąsdini žmones?! Skaitysiu tik rytoj, nes prieš miegą negalima – sapnuosis… Bet neabejoju, kad matematikos genijai neklysta.
matematikui: 100 balų už išradingą pateikimą, bet irgi skaitysiu tik rytoj; atrodo įtartinai…
D., 2010-02-02 22:23:29
iš manęs matematikas ne koks, bet galvojant ūkiškai pervertus trikampį ABC, kad 45 laipsnių kampas būtų priešingame kvadrato kampe, matysime jog trikampį įstrižainė kerta tose pačiose vietose 🙂
GL, 2010-02-02 22:26:52
matematikui:
grazus sprendimas (tikriausiai 3 ar 5 kartus trumpesnis uz mano:))
Tik nesupratau prie ko cia AA’ ir simetrijos asis… Paprasciausiai kas buvo padaryta su AB ir A’B’ galima analogiskai padaryti virsuje nubreziant FC’, lygiagrecia AC
GL, 2010-02-02 22:41:55
Siaip man geda, kad pamirsau S=0.5absin(ab) ploto formule… Ja naudojant, mano sprendimas irgi galetu buti trumpesnis ir paprastesnis:
AD = x/sin(a), AC = 1/cos(a)
AE = y/sin(45-a), AB = 1/cos(45-a)
AB*AC/(AD*AE) = tan(a) tan(45-a)/(xy) = (1+tan(a))(1+tan(45-a)) = (1+tan(a))(1+(1-tan(a))/(1+tan(a))) = 2
dominykas, 2010-02-02 23:17:06
Povilai, lygiai tokį patį kvadratėlį į vieną žymiausių savo paveikslų lyg tarp kitko įtapė toks renesanso dailininkas vokietis A. Diureris: http://en.wikipedia.org/wiki/Melencolia_I
Tiesa, jo kvadratėlis pasižymi dar keletu gražių savybių…
- Suma lygi 34 ne tik horizontaliose ir vertikaliose eilutėse bei visuose stulpeliuose, bet ir:
1a) Bet kuriame iš keturių kampinių 2×2 kvadratėlių;
1b) Centriniame 2×2 kvadratėlyje;
1c) Susumavus bet kurio 3×3 kvadrato kampinius langelius;
1d) Susumavus bet kurio ‘pasvirusio kvadrato’ kampinius langelius (pvz 3,8,9 ir 14)
1e) Imant bet kurį iš dviejų įsivaizduojamų lotyniškų kryžių (pvz, 3,5,11,15).
-
Kvadrato apatinė eilutė – paveikslo autoriaus ‘parašas’ – kampuose 4 ir 1 reiškia ketvirtąją ir pirmąją lotynų abėcėlės raides D ir A, kurios yra autoriaus inicialai, per vidurį – 1514, paveikslo nutapymo metai.
-
O dabar smagiausia dalis – susumavus visus kvadrato skaičius, gauname 136. Dabar užrašykime autoriaus vardą lotyniškai – ‘Albrecht Dvrer’, ir analogiškai pagal lotynų abėcelę priskirkime kiekvienai raidei paeiliui atitinkamą skaičių. Gausime, A-1, L-12, B – 2 ir t. t. Kas atspės, koks skaičius gaunamas, šitaip susumavus raides?:)
tai vat, koks smagus aštuntokiškas uždavinys..
dominykas, 2010-02-02 23:26:43
ojėi, kaip 1) punkte nusikalbėjau, na, bet turbūt gan aišku, kas ten turi būt..:)
matematikas, 2010-02-03 09:36:21
GL aciu uz pastaba. Pasirodo zodzio simetriskas paprasciau ir nevartot 🙂
Beje, dabar tavo sprendimas taip “suplonejo”, kad jau tumpesnis uz manaji 🙂
http://picasaweb.google.com/matematikas/BurgisForumas#5433915344648230850
Burgis, 2010-02-03 11:35:29
Ačiū, “matematikas” ir GL temą užbaigė. Nors “matematiko” sprendime yra šiokių tokių rašto klaidelių, bet esmė teisinga – trikampių panašumo santykiai.
Dabar parašysiu, kodėl įdėjau šį uždavinį. Aš nepritariu nuostatai, kad mokykloje reikia visus mokyti spręsti galvosūkius arba tokio, kaip šis, tipo uždavinius. Manau, kad mokykloje visi turi būti mokomi klasikos, o labiausiai – klasikinių principų. Nemėgstu, kai kas nors kitur nusižiūrėjęs sprendimą (o ne pats sugalvojęs!), pateikia uždavinį ir mėgaujasi, kad ne visi jį gali išspręsti. Taip galima dirbti tik su olimpiadų dalyviais, su pretenduojančiais studijuoti matematiką. Kitiems – matematikos Mocartas, nieko daugiau…
GL, 2010-02-03 16:20:21
Negi rimtai sitas uzdavinys buvo matematikos pamokoje (ir ne olimpiadininkams?) Sakyciau man cia panasu i koki miesto olimpiados lygi.
Jei taip, tai sutinku, kad nereiketu. Na nebent mokytojas pries duodamas uzdavini kalbejo apie metodus, kurie butent ir naudojami ji isspresti…
Rokas, 2010-03-11 15:12:47
Mokytojai turi savo mokymo technikų, kartais ištraukia kokį sudėtingesnį uždavinėlį tam, kad galėtų pasirodyti gabiausieji. Galbūt tai būna tam tikra motyvacija mažiau pažangiems.